Question

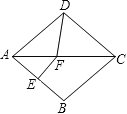
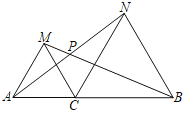
【题目】如图，点C为线段AB上一点，△ACM与△CBN都是等边三角形，AN与MB交于P．

（1）求证：AN＝BM；

（2）连接CP，求证：CP平分∠APB．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）由“SAS”可证△ACN≌△MCB，可得AN＝BM；

（2）过点C作CE⊥AN于点E，作CF⊥BM于点F，由全等三角形的性质可得S△ACN＝S△MCB，由三角形的面积相等，可得CE＝CF，由角平分线的性质定理的逆定理，即可得结论．

（1）∵△ACM与△CBN都是等边三角形，

∴AC＝CM，CN＝CB，∠ACM＝∠BCN＝60°，

∴∠ACN＝∠BCM＝120°，且AC＝CM，CN＝CB，

∴△ACN≌△MCB（SAS），

∴AN＝BM；

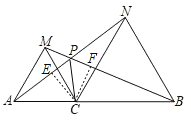
（2）过点C作CE⊥AN于点E，作CF⊥BM于点F，

∵△ACN≌△MCB，

∴S△ACN＝S△MCB，

∴×AN×CE＝×BM×CF，且AN＝BM，

∴CE＝CF，且CE⊥AN，CF⊥BM，

∴CP平分∠APB．