题目内容
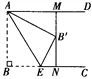
【题目】如图,AC是![]() 的直径,BC切
的直径,BC切![]() 于点C,AB交
于点C,AB交![]() 于点D,BC的中点为E,连接DE.
于点D,BC的中点为E,连接DE.
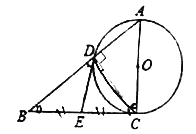
(1)求证:![]()
(2)连接E0交![]() 于点F填空:
于点F填空:
①当![]() __________时,以D,E,C,O为顶点的四边形是正方形;
__________时,以D,E,C,O为顶点的四边形是正方形;
②当![]() ______________时,以A,D,E,O为顶点的四边形是平行四边形
______________时,以A,D,E,O为顶点的四边形是平行四边形
【答案】(1)答案见解析;(2)①45°;②45°
【解析】
(1)根据直径所对的圆周角和直角三角形斜边中线的性质即可证明;(2)①如图,当∠B=45°时,以D,E,C,0为顶点的四边形是正方形;根据直径所对的圆周角是90°和全等三角形的判定先证△EOD≌△EOC,再结合(1)和∠B=45°,即可证四边形为正方形;②如图,利用①可证DE=OA,DE∥OA即可.
证明:(1)∵AC是直径
∴∠ADC=90°
∴∠BDC=90°
∴△BCD是直角三角形
又∵BE=CE
∴DE=CE=BE
∴BE=DE
(2)①连接OE,OD,如图,当∠B=45°时,以D,E,C,O为顶点的四边形是正方形
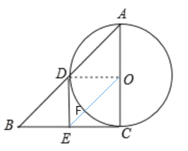
理由:∵BC是![]() 的切线
的切线
∴AC⊥BC,∠ACB=90°
∵OD=OC,OE=OE,DE=CE
∴△EOD≌△EOC(SSS)
∴∠EDO=∠ECO=90°
∵EB=ED
∴∠B=∠EDB=45°
∴∠DEC=∠B+∠EDB=90°
∴四边形DECO是矩形
∵OD=OC
∴矩形DECO是正方形
故答案为45°;
②如下图,结论∠B=45°

理由:当∠B=45°时,由①可知四边形DECO是正方形
∴DE∥OC,DE=OC
∵OA=OC
∴DE=OA
∴DE=OA,且DE∥OA
∴四边形ADEO是平行四边形
故答案为45°.

练习册系列答案
相关题目