题目内容
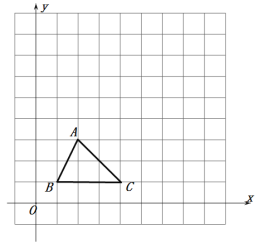
【题目】如图,在边长为1的小正方形网格中:
(1)![]() 向上平移6个单位长度,再向右平移5个单位长度后得到
向上平移6个单位长度,再向右平移5个单位长度后得到![]() ,则
,则![]() 的坐标为______;
的坐标为______;
(2)以点![]() 为位似中心,将
为位似中心,将![]() 放大为原来的2倍,得到
放大为原来的2倍,得到![]() ,请在网格中画出
,请在网格中画出![]() .
.
(3)![]() 的周长为_________________,面积为_________________.
的周长为_________________,面积为_________________.
【答案】(1)(9,7);(2)详见解析;(3)周长为:![]() +
+![]() +8,面积为
+8,面积为![]()
【解析】
(1)根据平移要求画图,再确定点的坐标;(2)根据位似要求画图;(3)根据图,求出关键线段的长度,再求周长和面积.
解:(1)将△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1,如图所示;![]() 的坐标为(9,7)
的坐标为(9,7)
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,如图所示.
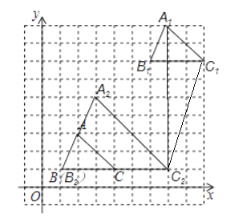
(3)根据(1),(2)图可得A1(7,9),C2(7,1)
所以A1C2=9-1=8,C1到A1C2的距离是9-7=2,
A1C1=![]() , C1C2=
, C1C2=![]()
所以![]() 的周长为:
的周长为:![]() +
+![]() +8,面积为
+8,面积为![]()

练习册系列答案
相关题目