题目内容
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

【答案】7200元.
【解析】
连接BD.在Rt△ABD中,根据勾股定理求得BD=5,在△CBD中,由勾股定理的逆定理判定∠DBC=90°,再由S四边形ABCD=S△BAD+S△DBC求得四边形ABCD的面积,由此即可求得所需费用.
如图,连接BD.
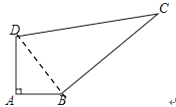
在Rt△ABD中,BD2=AB2+AD2=32+42=52,BD=5;
在△CBD中,CD2=132,BC2=122,而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() AD·AB+
AD·AB+![]() DB·BC=
DB·BC=![]() ×4×3+
×4×3+![]() ×5×12=36,
×5×12=36,
所以需费用36×200=7200(元).

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
【题目】一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 1000 |
摸到红球次数m | 151 | 221 | 289 | 358 | 429 | 497 | 568 | 701 |
摸到红球频率 | 0.75 | 0.74 | 0.72 | 0.72 | 0.72 | 0.71 | a | b |
(1)表格中a=________,b=_________;
(2)估计从袋子中摸出一个球恰好是红球的概率约为________;(精确到0.1)
(3)如果袋子中有14个红球,那么袋子中除了红球,还有多少个其他颜色的球?