题目内容
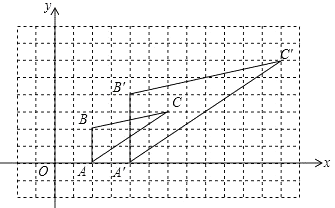
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A,B,C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1)请在图中画出一个△ ![]() ,使△
,使△ ![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△ ![]() 的面积。
的面积。
【答案】
(1)解:∵A(2,0)、B(2,2)、C(6,3),△A′B′C′与△ABC是以坐标原点为位似中心,相似比为2的位似图形,
∴A′(4,0),B′(4,4),C′(12,6),如图:
(2)解:S△A′B′C′= ![]() ×4×8=16
×4×8=16
【解析】(1)分别连接OB、OA,并延长至B',A',C',使OB'=2OB,OA'=2OA,OC'=2OC,顺次连接A'、B'、C';(2)利用面积公式即可算出.
【考点精析】解答此题的关键在于理解位似变换的相关知识,掌握它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心),以及对作图-位似变换的理解,了解对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.

练习册系列答案
相关题目