题目内容
【题目】 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
(1)如图1,求证:A、G、E、F四点围成的四边形是菱形;
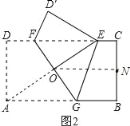
(2)如图2,点N是线段BC的中点,且ON=OD,求折痕FG的长.

【答案】(1)证明见解析;(2)折痕FG的长是![]() .
.
【解析】
(1)根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而判断出EF=AG,得出四边形AGEF是平行四边形,继而结合AG=GE,可得出结论.
(2)连接ON,得出ON是梯形ABCE的中位线,设CE=x,在RT△ADE中,利用勾股定理可解出x,继而可得出折痕FG的长度.
(1)证明:由折叠的性质可得,GA=GE,∠AGF=∠EGF,
∵DC∥AB,
∴∠EFG=∠AGF,
∴∠EFG=∠EGF,
∴EF=EG=AG,
∴四边形AGEF是平行四边形(EF∥AG,EF=AG),
又∵AG=GE,
∴四边形AGEF是菱形.
(2)解:连接ON,
∵O,N分别是AE,CB的中点,
故ON是梯形ABCE的中位线,
设CE=x,则ED=4﹣x,2ON=CE+AB=x+4,
在Rt△AED中,AE=2OE=2ON=x+4,
AD2+DE2=AE2,
∴22+(4﹣x)2=(4+x)2,
得x=![]() ,
,
OE=![]() ,
,
∵△FEO∽△AED,
∴![]() ,
,
解得:FO=![]() ,
,
∴FG=2FO=![]() .
.
故折痕FG的长是![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目