题目内容
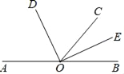
【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 ![]() .
.
(1)求证:∠BAE=∠CAD;
(2)求证:△ABE∽△ACD.
【答案】
(1)证明:在△ABC与△AED中,
∵ ![]() ,
,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAC﹣∠EAF=∠EAD﹣∠EAF,
即∠BAE=∠CAD;
(2)解:∵ ![]() ,
,
∴ ![]() ,
,
在△ABE与△ACD中,
∵∠BAE=∠CAD, ![]() ,
,
∴△ABE∽△ACD.
【解析】(1)根据相似三角形的判定方法三边对应成比例,两三角形相似,得到△ABC∽△AED,得到对应角相等,根据角的和差证明出∠BAE=∠CAD;(2)根据比例的性质得到两边对应成比例,再由夹角相等,得到两三角形相似.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
相关题目