题目内容
已知:抛物线y=ax2+bx+4的对称轴为x=-1,且与x轴相交于点A、B,与y轴相交于点C,其中点A的坐标为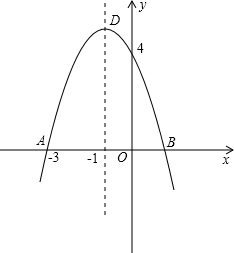 (-3,0),
(-3,0),
(1)求该抛物线的解析式;
(2)若该抛物线的顶点为D,求△ACD的面积;
(3)在抛物线的对称轴上是否存在点P,使得以A、B、C、P为顶点的四边形是梯形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
 (-3,0),
(-3,0),(1)求该抛物线的解析式;
(2)若该抛物线的顶点为D,求△ACD的面积;
(3)在抛物线的对称轴上是否存在点P,使得以A、B、C、P为顶点的四边形是梯形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)由题意得
,
解得
∴抛物线的解析式为y=-
x2-
x+4.
(2)∵D是抛物线y=-
x2-
x+4的顶点
∴点D的坐标为(-1,
)
设AC与抛物线对称轴的交点为E
∴DE=
-
=
∴S△ACD=S△CDE+S△ADE=
×
×2+
×
×1=4.
(3)设抛物线的对称轴与x轴的交点为H
若PC∥AB,则点P(-1,4);
若PB∥AC,△PHB∽△COA,
∴
=
,即
=
,
解得PH=
.
∴P(-1,-
);
若PA∥BC,则△PHA∽△COB,
∴
=
,
即
=
,
解得PH=8
∴P(-1,-8).
因此符合条件的P点有三个:(-1,4);(-1,-
);(-1,-8).
|
解得
|
∴抛物线的解析式为y=-
| 4 |
| 3 |
| 8 |
| 3 |
(2)∵D是抛物线y=-
| 4 |
| 3 |
| 8 |
| 3 |
∴点D的坐标为(-1,
| 16 |
| 3 |
设AC与抛物线对称轴的交点为E
∴DE=
| 16 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
∴S△ACD=S△CDE+S△ADE=
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
(3)设抛物线的对称轴与x轴的交点为H
若PC∥AB,则点P(-1,4);
若PB∥AC,△PHB∽△COA,
∴
| PH |
| CO |
| BH |
| AO |
| PH |
| 4 |
| 2 |
| 3 |
解得PH=
| 8 |
| 3 |
∴P(-1,-
| 8 |
| 3 |
若PA∥BC,则△PHA∽△COB,
∴
| PH |
| CO |
| AH |
| BO |
即
| PH |
| 4 |
| 2 |
| 1 |
解得PH=8
∴P(-1,-8).
因此符合条件的P点有三个:(-1,4);(-1,-
| 8 |
| 3 |

练习册系列答案
相关题目