题目内容
【题目】问题提出:在矩形ABCD中,AB=6,BC=4,点E、F分别为边AD、BC上的点,且AE=1;BF=2.
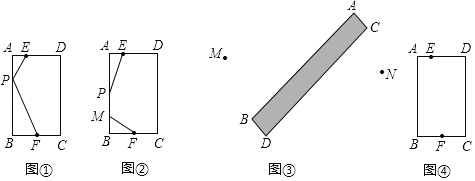
(1)如图①,P为边AB上一动点,连接EP、PF,则EP+PF的最小值为_____;
(2)如图②,P、M是AB边上两动点,且PM=2,现要求计算出EP、PM、MF和的最小值.九年级一班某兴趣小组通过讨论得出一个解决方法:在DA的延长线上取一点E',使AE'=AE,再过点E'作AB的平行线E'C,在E'C上E”的下方取点M,使E'M'=2,连接M'F,则与AB边的交点即为M,再在边AB上点M的上方取P点,且PM=2,此时EP+PM+MF的值最小.但他们不确定此方法是否可行,便去请教数学田老师,田老师高兴地说:“你们的做法是有道理的”.现在请你根据叙述作出草图并计算出EP+PM+MF的最小值;
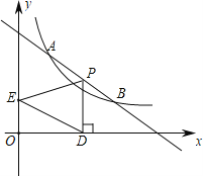
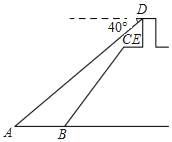
问题解决:(3)聪聪的爸爸是供电公司的线路设计师,公司准备架设一条经过农田区的输电线路,为M、N两个村同时输电.如图所示,农田区两侧AB与CD平行,且农田区宽为0.5千米,M村到AB的距离为2千米,N村到CD的距离为1千米,M、N所在的直线与AB所夹锐角恰好为45°,根据架线要求,在农田区内的线路要与AB垂直.请你帮助聪聪的爸爸设计出最短的线路图,并计算出最短线路的长度.(要求:写出计算过程,结果保留根号)
【答案】(1)![]() ;(2)EP+PM+MF的最小值是7;(3)
;(2)EP+PM+MF的最小值是7;(3)![]() km
km
【解析】
(1)利用轴对称方法求最短路线,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 或作点
或作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,则
,则![]() 即为最小值;
即为最小值;
(2)由于PM是定值,可以通过平移点的方式将问题转化为问题一,再通过对称求最短路线;
(3)由于农田的宽度一定,故可将M点延AB的垂直方向移动农田的宽度到![]() ,将问题转化为两点之间线段最短问题即可,作
,将问题转化为两点之间线段最短问题即可,作![]() ,并在
,并在![]() 上截取
上截取![]() (农田的宽度),连接
(农田的宽度),连接![]() 交
交![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 即为最短路线.
即为最短路线.
解:(1)如图①,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
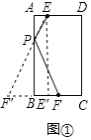
![]() 矩形
矩形![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
当![]() ,
,![]() ,
,![]() 三点共线时,
三点共线时,![]() 最小,即
最小,即![]() 最小;
最小;
由勾股定理得:![]() ,
,
故答案为![]() ;
;
(2)如图②,延长![]() 至
至![]() ,使
,使![]() ,在
,在![]() 下方作
下方作![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,![]() ,
,
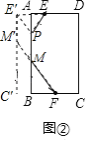
![]() 矩形
矩形![]()
![]() ,即
,即![]() ,
,
![]()
![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
![]() 为最小值,
为最小值,
即![]() 为最小值.
为最小值.
(3)如图③,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,
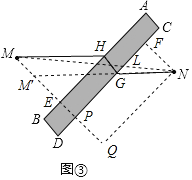
在![]() 上截取
上截取![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
由题意知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
在![]() △
△![]() 中,
中,![]() ,
,
![]()
![]() 最短线路长度为
最短线路长度为![]() .
.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案