��Ŀ����
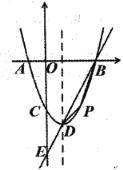
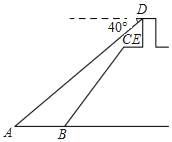
����Ŀ����ͼ��С��վ�ڽ���ij�t��̨DE�Ķ���D������ý����ϵ��洬A�ĸ���Ϊ40�������t��̨DE��ֱ�ڽ��棬���ĸ߶�Ϊ3�ף�CE��2�ף�CEƽ���ڽ���AB��ӭˮ��BC���¶�i��1��0.75���³�BC��10�ף�
���ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84��cot40���1.19��
��1����t��̨DE�Ķ���D������AB�ľ��룻
��2�����洬A��ӭˮ��BC�ĵ�B�ľ��룮���������һλС����
���𰸡���1���t��̨DE�Ķ���D������AB�ľ���Ϊ11�ף�2���洬A��ӭˮ��BC�ĵ�B�ľ���Ϊ5.1��
��������
��1���ӳ�DE��AB�ڵ�F������C��CG��AB������Ϊ��G�������¶ȱ�ʾ��CG��BG�ij�����������𰸣�
��2����Rt��ADF�У�����cotA��![]() ���ó�AF�ij��������ó��𰸣�
���ó�AF�ij��������ó��𰸣�
��1���ӳ�DE��AB�ڵ�F������C��CG��AB������Ϊ��G��

�������֪CE��GF��2��CG��EF
��Rt��BCG����BGC��90����
��i��![]() ��
��
��CG��4k��BG��3k����BC��![]() =5k��10��
=5k��10��
��k��2��
��BG��6����CG��EF��8��
��DE��3����DF��DE+EF��3+8��11���ף���
�𣺲t��̨DE�Ķ���D������AB�ľ���Ϊ11�ף�
��2��������á�A��40����
��Rt��ADF����DFA��90����
��cotA��![]() ��
��
��![]() ��1.19��
��1.19��
��AF��11��1.19��13.09��m����
��AB��AF��BG��GF��5.09��5.1���ף���
���洬A��ӭˮ��BC�ĵ�B�ľ���Ϊ5.1�ף�

 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�