题目内容
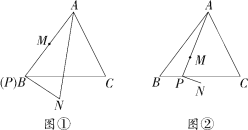
【题目】如图,在△ABC中,AB=BC=10,tan∠ABC=![]() ,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
(1)如图①,当点P在点B,点M是AP中点时,试求AN的长;
(2)如图②,当![]() =
=![]() 时,
时,
①求点N到BC边的距离(用含t的代数式表示);
②当点P从点B运动至点C时,试求点N运动路径的长.
【答案】(1)![]() ;(2)①当0≤t≤6时,
;(2)①当0≤t≤6时,![]() ,当6≤t≤10时,
,当6≤t≤10时,![]() ;②
;②![]()
【解析】
(1)根据直角三角形中的勾股定理进行解答即可;
(2)①分0≤t≤6和6≤t≤10两种情况,利用相似三角形进行解答;
②利用勾股定理进行计算即可.
(1)∵在Rt△ABN中,∠ABN=90°,AB=10,
∴BN=BM=![]() AB=5,
AB=5,
∴AN=![]() =
=![]() ;
;
(2)①(Ⅰ)当0≤t≤6时(如图①),
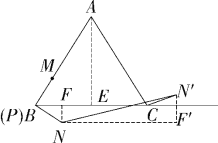
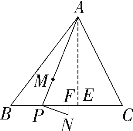
图①图②
如解图:过点A作AE⊥BC于点E,过点N作NF⊥BC于点F,
∵tan∠ABC=![]() =
=![]() ,设AE=4x,则BE=3x,
,设AE=4x,则BE=3x,
在Rt△ABE中,∠AEB=90°,
∴AB2=AE2+BE2,102=(3x)2+(4x)2,
解得:x=2,∴AE=8,BE=6
当0≤t≤6时.
∵∠AEP=∠PFN=90°,∠APE+∠FPN=90°,∠APF+∠PAE=90°,
∴∠PAE=∠FPN,
∴△APE∽△PNF,
∵![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() ;
;
(Ⅱ)当6≤t≤10时,
同理可得:![]()
②如图②点N的运动路径是一条线段,
当P与O重合时,FN=![]() ,PF=2,
,PF=2,
当P与C重合时,F′N′=1,CF′=2,
∴点N的路径长NN′=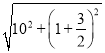 =
=![]() .
.

【题目】为了解某区2014年八年级学生的体育测试情况,随机抽取了该区若干名八年级学生的测试成绩进行了统计分析,并根据抽取的成绩等级绘制了如下的统计图表![]() :
:
成绩等级 | A | B | C | D |
人数 | 60 | 10 |
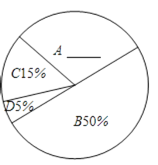
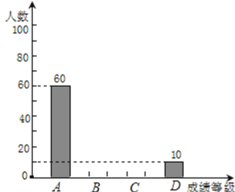
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有______ 名,成绩为B类的学生人数为______ 名,C类成绩所在扇形的圆心角度数为______
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该区约5000名八年级学生体育测试成绩为D类的学生人数.