题目内容
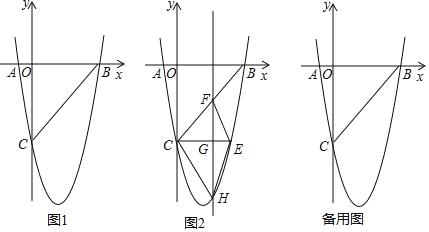
【题目】在平面直角坐标系xOy中,我们把以抛物线![]() 上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为
上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”.如图,已知某条“子抛物线”的二次项系数为![]() ,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
,且与y轴交于点C.设点A的横坐标为m(m>0),过点A作y轴的垂线交y轴于点B.
(1)当m=1时,求这条“子抛物线”的解析式;
(2)用含m的代数式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)m的值为2
;(3)m的值为2
【解析】
(1)先求出m=1时点A的坐标,进而可得到这条“子抛物线”的解析式;
(2)先根据A点坐标求出“子抛物线”的解析式和AB,OB的长度,然后令x = 0求出y值即可得到C点坐标,进而可求出BC的长度,最后利用![]() 即可求解;
即可求解;
(3)过O点作OD⊥CA的延长线于点D,过点D作y轴的平行线分别交BA的延长线于点E,交x轴于点F, 首先证明△AED≌△DFO,则有AE=DF,DE=OF,设AE=n,那么DF=n,BE= m + n=OF=ED,通过OB=EF得到![]() ,然后再通过
,然后再通过![]() 得到
得到![]() ,将两个关于m,n的方程联立即可求出m的值.
,将两个关于m,n的方程联立即可求出m的值.
解:(1)∵点A在![]() 上,点A的横坐标为m,
上,点A的横坐标为m,
∴A(m,m2),
当m =1时,![]() ,
,
∴A(1,1),
∴这条“子抛物线”的解析式为![]() .
.
(2)由A(m,m2),且AB⊥y轴,可得AB=m,OB= m2.
∴“子抛物线”的解析式为![]() .
.
令x = 0,![]() ,
,
∴点C的坐标(0,![]() ),
),![]() ,
,
∴![]() .
.
在Rt△ABC中,
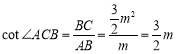 .
.
(3)如图,过O点作OD⊥CA的延长线于点D,过点D作y轴的平行线分别交BA的延长线于点E,交x轴于点F.
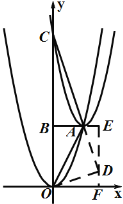
∵∠OAC=135°,
∴∠OAD=45°.
又∵OD⊥CA,
![]()
∴∠AOD=∠OAD=45°,
∴AD=OD,
![]() ,
,
![]() .
.
![]() ,
,
∴△AED≌△DFO,
∴AE=DF,DE=OF.
设AE=n,那么DF=n,BE= m + n=OF=ED.
又∵OB=EF,
∴![]() .
.
又![]() ,
,
∴∠BCA=∠ADE,
∴![]() .
.
解方程组 ,得
,得![]() ,
,![]() (舍去)
(舍去)
∴ m的值为2.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案