题目内容
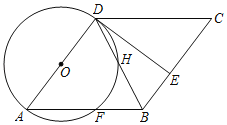
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:△DAF≌△DCE.
(2)求证:DE是⊙O的切线.
(3)若BF=2,DH=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)20.
【解析】
(1)连接DF,结合菱形的性质利用SAS可证△DAF≌△DCE;
(2)由直径所对的圆周角是直角可知∠DFA=90°,由全等的性质与平行的性质可得∠ADE=90°,根据切线的判定定理可得结论;
(3)连接AH,由等腰三角形三线合一的性质可得DB=2DH,根据勾股定理可得AD、AF、DF长,易得四边形ABCD的面积.
(1)证明:如图,连接DF,
∵四边形ABCD为菱形,
∴AB=BC=CD=DA,AD∥BC,∠DAB=∠C,
∵BF=BE,
∴AB﹣BF=BC﹣BE,
即AF=CE,
∴△DAF≌△DCE(SAS);
(2)由(1)知,△DAF≌△DCE,则∠DFA=∠DEC.
∵AD是⊙O的直径,
∴∠DFA=90°,∴∠DEC=90°
∵AD∥BC,
∴∠ADE=∠DEC=90°,
∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(3)解:如图,连接AH,
∵AD是⊙O的直径,
∴∠AHD=∠DFA=90°,
∴∠DFB=90°,
∵AD=AB,DH=![]() ,
,
∴DB=2DH=2![]() ,
,
在Rt△ADF和Rt△BDF中,
∵DF2=AD2﹣AF2,DF2=BD2﹣BF2,
∴AD2﹣AF2=DB2﹣BF2,
∴AD2﹣(AD﹣BF)2=DB2﹣BF2,
∴AD2﹣(AD﹣2)2=(2![]() )2﹣22,
)2﹣22,
∴AD=5.
∴AH=![]() =
=![]() =2
=2![]() ,
,
∴S四边形ABCD=2S△ABD=2×![]() AH=BDAH=2
AH=BDAH=2![]() ×2
×2![]() =20.即四边形ABCD的面积是20,
=20.即四边形ABCD的面积是20,
故答案为:20.

 名校课堂系列答案
名校课堂系列答案【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

根据以上信息,整理分析数据如下:
平均月收/千元 | 中位数/千元 | 众数/千元 | 方差/千元 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空:①__________②__________③__________
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.