题目内容
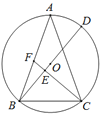
【题目】已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连结EM,分别交线段AD、AC于点F、G.
(1)求证:![]() ;
;
(2)当BC2=2BABE时,求证:∠EMB=∠ACD.
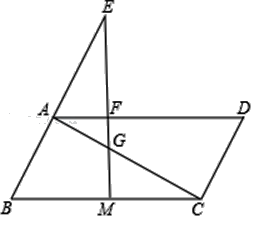
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据题意可得四边形ABCD是平行四边形,易证△FGA∽△MGC ,△EAF∽△EBM,再利用相似三角形的性质与等量代换即可得证;
(2)将BC2=2BABE变形为![]() ,根据相似三角形的判定可得△BCA∽△BEM,则∠BME=∠BAC,再根据平行四边形的性质即可得证.
,根据相似三角形的判定可得△BCA∽△BEM,则∠BME=∠BAC,再根据平行四边形的性质即可得证.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴ △FGA∽△MGC ,△EAF∽△EBM,
∴![]() ,
,![]() ,
,
∵M是BC边的中点,
∴CM=BM,
∴![]() ,
,
∴![]() ;
;
(2)∵BC2=2BABE,
∴![]() ,
,
∵∠B=∠B,
∴△BCA∽△BEM,
∴∠BME=∠BAC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
∴∠EMB=∠ACD.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目