题目内容
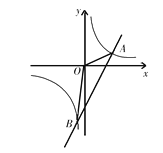
【题目】在菱形ABCD中,点P、Q分别在BC、CD上,∠PAQ=∠B.
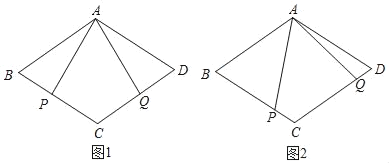
(1)如图1,若AP⊥BC,求证:AP=AQ;
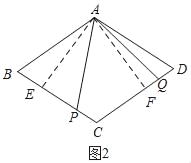
(2)如图2,若点P为BC上一点,AP=AQ仍成立吗?请说明理由.
【答案】(1)成立;(2)成立,见解析
【解析】
(1)根据题意可利用菱形的性质证明△ABP≌△ADQ(AAS)即可解答
(2)过点A作AE⊥BC于点E,AF⊥CD于点F,在证明△AEP≌△AFQ(ASA)即可解答
(1)在菱形ABCD中,
∠B+∠C=180°,AB=AD,∠B=∠D,
∵∠PAQ=∠B,
∴∠PAQ+∠C=180°,
∴∠APC+∠AQC=180°,
∵AP⊥BC,
∴∠APB=∠AQD=90°,
在△ABP与△ADQ中,
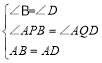 ,
,
∴△ABP≌△ADQ(AAS),
∴AP=AQ;
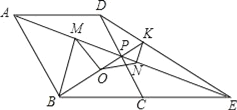
(2)过点A作AE⊥BC于点E,AF⊥CD于点F,
由(1)可知:AE=AF,∠PAQ=∠B=∠EAF,
∴∠EAP=∠FAQ,
在△AEP与△AFQ中,
![]()
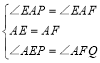 ,
,
∴△AEP≌△AFQ(ASA),
∴AP=AQ.

练习册系列答案
相关题目