ƒøƒ⁄»ð
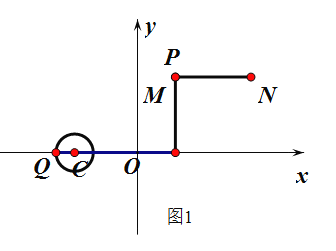
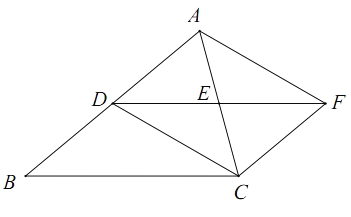
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨∂‘”⁄»Œ“‚¡Ωµ„
÷–£¨∂‘”⁄»Œ“‚¡Ωµ„![]() £¨
£¨![]() £¨»Áπ˚
£¨»Áπ˚![]() £¨‘Ú≥∆
£¨‘Ú≥∆![]() ”Î
”Î![]() ª•Œ™°∞
ª•Œ™°∞![]() æýµ„°±£Æ¿˝»Á£∫µ„
æýµ„°±£Æ¿˝»Á£∫µ„![]() £¨µ„
£¨µ„![]() £¨”…
£¨”…![]() £¨ø…µ√µ„
£¨ø…µ√µ„![]() ”Î
”Î![]() ª•Œ™°∞
ª•Œ™°∞![]() æýµ„°±£Æ
æýµ„°±£Æ
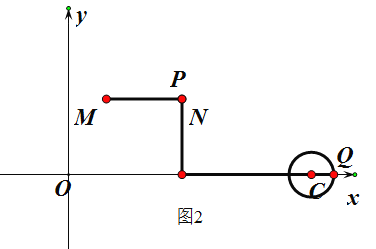
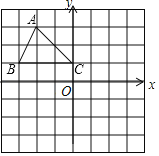
£®1£©‘⁄µ„![]() £¨
£¨![]() £¨
£¨![]() ÷–£¨‘≠µ„
÷–£¨‘≠µ„![]() µƒ°∞
µƒ°∞![]() æýµ„°± «_____(ÃÓ◊÷ƒ∏)£ª
æýµ„°± «_____(ÃÓ◊÷ƒ∏)£ª
£®2£©“—÷™µ„![]() £¨µ„
£¨µ„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜∆Ω––”⁄
◊˜∆Ω––”⁄![]() ÷·µƒ÷±œþ
÷·µƒ÷±œþ![]() £Æ
£Æ
¢Ÿµ±![]() ±£¨÷±œþ
±£¨÷±œþ![]() …œµ„
…œµ„![]() µƒ°∞
µƒ°∞![]() æýµ„°±µƒ◊¯±ÍŒ™_____£ª
æýµ„°±µƒ◊¯±ÍŒ™_____£ª
¢⁄»Ù÷±œþ![]() …œ¥Ê‘⁄µ„
…œ¥Ê‘⁄µ„![]() µƒ°∞
µƒ°∞![]() µ„°±£¨«Û
µ„°±£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
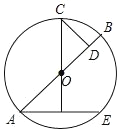
£®3£©“—÷™µ„![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() µƒ∞Îæ∂Œ™
µƒ∞Îæ∂Œ™![]() £¨»Ù‘⁄œþ∂Œ
£¨»Ù‘⁄œþ∂Œ![]() …œ¥Ê‘⁄µ„
…œ¥Ê‘⁄µ„![]() £¨‘⁄
£¨‘⁄![]() …œ¥Ê‘⁄µ„
…œ¥Ê‘⁄µ„![]() £¨ πµ√µ„
£¨ πµ√µ„![]() ”ε„
”ε„![]() ª•Œ™°∞
ª•Œ™°∞![]() æýµ„°±£¨÷±Ω”–¥≥ˆ
æýµ„°±£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©¢Ÿ
£ª£®2£©¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª£®3£©
£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð∂®“Â≈–∂œº¥ø…£ª
£®2£©¢Ÿ…Ë÷±œþ![]() …œ”ε„
…œ”ε„![]() µƒ°∞
µƒ°∞![]() æýµ„°±µƒµ„µƒ◊¯±ÍŒ™£®a£¨3£©£¨∏˘æð∂®“¡–≥ˆπÿ”⁄aµƒ∑Ω≥ã¨Ω‚∑Ω≥ú¥ø…£ª
æýµ„°±µƒµ„µƒ◊¯±ÍŒ™£®a£¨3£©£¨∏˘æð∂®“¡–≥ˆπÿ”⁄aµƒ∑Ω≥ã¨Ω‚∑Ω≥ú¥ø…£ª
¢⁄µ„![]() ◊¯±ÍŒ™
◊¯±ÍŒ™![]() £¨÷±œþ
£¨÷±œþ![]() …œµ„µƒ◊ð◊¯±ÍŒ™b£¨”…“‚µ√
…œµ„µƒ◊ð◊¯±ÍŒ™b£¨”…“‚µ√![]() £¨◊™ªØŒ™≤ªµ» Ω◊È£¨Ω‚≤ªµ» Ω◊Ⱥ¥ø…£Æ
£¨◊™ªØŒ™≤ªµ» Ω◊È£¨Ω‚≤ªµ» Ω◊Ⱥ¥ø…£Æ
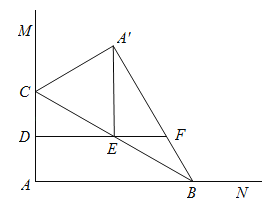
£®3£©∑÷¿ýÃ÷¬€£¨∑÷±»°P”ε„M÷ÿ∫œ°¢P”ε„N÷ÿ∫œÃ÷¬€°£µ±µ„P”ε„M÷ÿ∫œ ±£¨…Ë°—C◊Û≤ý”Îx÷·Ωª”⁄µ„Q£¨‘Úµ„Qµƒ◊¯±Í «£®m-![]() £¨0£©£¨∏˘æð∂®“¡–≥ˆπÿ”⁄mµƒæ¯∂‘÷µ∑Ω≥ã¨Ω‚∑Ω≥㨻°Ωœ–°µƒ÷µ£ªµ±µ„P”ε„N÷ÿ∫œ ±£¨…Ë°—C”“≤ý”Îx÷·Ωª”⁄µ„Q£¨‘Úµ„Qµƒ◊¯±Í «£®m+
£¨0£©£¨∏˘æð∂®“¡–≥ˆπÿ”⁄mµƒæ¯∂‘÷µ∑Ω≥ã¨Ω‚∑Ω≥㨻°Ωœ–°µƒ÷µ£ªµ±µ„P”ε„N÷ÿ∫œ ±£¨…Ë°—C”“≤ý”Îx÷·Ωª”⁄µ„Q£¨‘Úµ„Qµƒ◊¯±Í «£®m+![]() £¨0£©£¨∏˘æð∂®“¡–≥ˆπÿ”⁄mµƒæ¯∂‘÷µ∑Ω≥ã¨Ω‚∑Ω≥㨻°Ωœ¥Ûµƒ÷µ£¨Œ µ√Ω‚£Æ
£¨0£©£¨∏˘æð∂®“¡–≥ˆπÿ”⁄mµƒæ¯∂‘÷µ∑Ω≥ã¨Ω‚∑Ω≥㨻°Ωœ¥Ûµƒ÷µ£¨Œ µ√Ω‚£Æ
Ω‚£∫£®1£©°þ![]() £¨O£®0,0£©£¨
£¨O£®0,0£©£¨
°ý![]() £¨
£¨
°ýµ„D”Α≠µ„ª•Œ™°∞![]() æýµ„°±£ª
æýµ„°±£ª
°þ![]() £¨O£®0,0£©£¨
£¨O£®0,0£©£¨
°ý![]() £¨
£¨
À˘“‘µ„D”Α≠µ„ª•Œ™°∞![]() æýµ„°±£ª
æýµ„°±£ª
°þ![]() £¨O£®0,0£©£¨
£¨O£®0,0£©£¨
°ý![]() £¨
£¨
À˘“‘µ„D”Α≠µ„ª•Œ™°∞![]() æýµ„°±£ª
æýµ„°±£ª
π ¥∞∏Œ™£∫![]() £ª
£ª
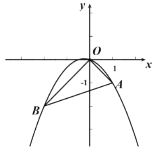
£®2£©¢Ÿ…Ë÷±œþ![]() …œ”ε„
…œ”ε„![]() µƒ°∞
µƒ°∞![]() æýµ„°±µƒµ„µƒ◊¯±ÍŒ™£®a£¨3£©£¨
æýµ„°±µƒµ„µƒ◊¯±ÍŒ™£®a£¨3£©£¨
‘Ú![]() £¨
£¨
Ω‚µ√a=2
π ¥∞∏Œ™£®2,3£©£ª
¢⁄»ÁÕº£¨µ„![]() ◊¯±ÍŒ™
◊¯±ÍŒ™![]() £¨÷±œþ
£¨÷±œþ![]() …œµ„µƒ◊ð◊¯±ÍŒ™b£¨…Ë÷±œþ
…œµ„µƒ◊ð◊¯±ÍŒ™b£¨…Ë÷±œþ![]() …œµ„µƒ◊¯±ÍŒ™£®c£¨b£©
…œµ„µƒ◊¯±ÍŒ™£®c£¨b£©
‘Ú£∫![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() ,
,
°ý![]() ,
,
º¥![]() µƒ»°÷µ∑∂Œß «
µƒ»°÷µ∑∂Œß «![]() £ª
£ª
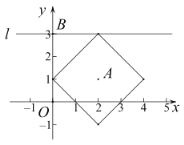
£®3£©»ÁÕº£®1£©£¨µ±µ„P”ε„M÷ÿ∫œ ±£¨…Ë°—C◊Û≤ý”Îx÷·Ωª”⁄µ„Q£¨‘Úµ„Qµƒ◊¯±Í «£®m-![]() £¨0£©£¨
£¨0£©£¨
°þµ„P”ε„Qª•Œ™°∞5-æýµ„"£¨P£®1,2£©£¨
°ý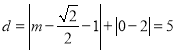 £¨
£¨
Ω‚µ√£∫![]() £¨
£¨![]() £ª
£ª
°þ![]() £¨
£¨
°ý»°![]() £Æ
£Æ
µ±µ„P”ε„N÷ÿ∫œ ±£¨…Ë°—C”“≤ý”Îx÷·Ωª”⁄µ„Q£¨‘Úµ„Qµƒ◊¯±Í «£®m+![]() £¨0£©£¨
£¨0£©£¨
°þµ„P”ε„Qª•Œ™°∞5-æýµ„"£¨‘ÚP£®3,2£©£¨
°ý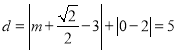 £¨
£¨
Ω‚µ√£∫![]() £¨
£¨![]() £¨
£¨
°þ![]()
°ý»°![]()
°ý![]() £Æ
£Æ