题目内容
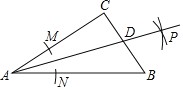
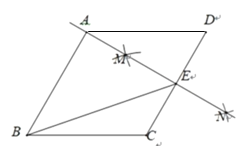
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
【答案】C
【解析】
连接AC,根据线段垂直平分线的性质及菱形的性质即可判断A选项正确;利用同底等高的性质证明△ABE的面积=△ABC的面积=△ACD的面积,再利用线段垂直平分线的性质即可判断B选项;根据线段垂直平分线的性质及菱形的性质求出∠BAE=90°,利用三角函数求出AE,即可利用勾股定理求出BE,由此判断C选项;过点E作EF⊥BC交延长线于F,利用三角函数求出EF,再利用勾股定理求出BF,由此判断D选项.
连接AC,
由题意知:MN垂直平分CD,
∴AC=CD,
∵四边形ABCD是菱形,
∴AD=AB=BC=CD,
∴AC=AD=CD=AB=BC,
∴△ABC和△ACD都是等边三角形,
∴∠BAC=∠CAD=∠ABC=60°,故A正确;
∵AE垂直平分CD,
∴∠CAE=∠DAE=30°,
∴∠BAE=90°,
∴![]() ,故B正确;
,故B正确;
∵AB=4,
∴AC=CD=4,
∴![]() ,
,
∴![]() ,故C错误;
,故C错误;
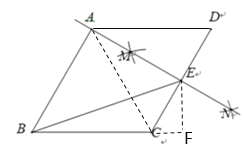
过点E作EF⊥BC交延长线于F,
∵∠ECF=180°-60°=120°,CE=2,
∴EF=![]() ,
,
∴BF=![]() ,
,
∴tanCBE![]() ,故D正确,
,故D正确,
故选:C.

【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?