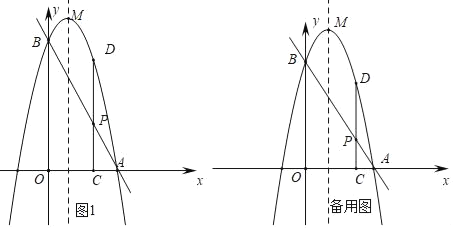
题目内容
【题目】如图,抛物线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() 将抛物线
将抛物线![]() 平移得到拋物线
平移得到拋物线![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
![]() 直接写出点
直接写出点![]() ,点
,点![]() 的坐标.
的坐标.![]() 求抛物线
求抛物线![]() 的表达式.
的表达式.
![]() 点
点![]() 是抛物线
是抛物线![]() 上
上![]() 间--点,作
间--点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连结
,连结![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() 当
当![]() 为何值时,使
为何值时,使![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.
【答案】![]() ;
;![]()
![]() ;
;![]()
![]() 时,
时,![]() 有最大值,且最大值为
有最大值,且最大值为![]() .
.
【解析】
(1)①过点B作BE⊥x轴于点E,过点C作CF⊥x轴于点F,则BE∥CF,根据平行线分线段成比例定理可得OE=EF=3,求出B(3,3)即可得C(6,6);
②把点B,C的坐标代入![]() 求出b,c即可;
求出b,c即可;
(2)求出![]() ,可得
,可得![]() ,再根据二次函数的性质求解可得.
,再根据二次函数的性质求解可得.
解:(1)①如图,过点B作BE⊥x轴于点E,过点C作CF⊥x轴于点F,则BE∥CF,
∵点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() ,
,
∴OE=EF=3,
当x=3时y=x2+4x=9+12=3,即B(3,3),
∴直线OB的解析式为:y=x,
∴C(6,6),
②把点B,C的坐标代入抛物线![]() 中,
中,
得![]() ,解得:
,解得:![]() ,
,
所以抛物线![]() 的解析式为:
的解析式为:![]() ;
;
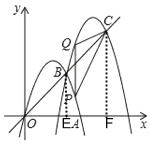
(2) ![]() 轴,点
轴,点![]() 的横坐标为
的横坐标为![]() ,
,
∴P(m,m2+4m),Q(m,![]() ),
),
![]() ,
,
![]() ,
,
由于![]() 是抛物线
是抛物线![]() 上
上![]() 段一点,易知A(4,0),
段一点,易知A(4,0),
故![]() ,
,
而![]() 不在
不在![]() 的范围内,且
的范围内,且![]() 开口向下,在对称轴的左侧,
开口向下,在对称轴的左侧,![]() 随着
随着![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.

练习册系列答案
相关题目