题目内容
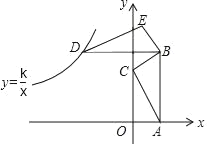
【题目】如图所示,已知点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,![]() 轴于点
轴于点![]() 连结
连结![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的面积比为( )
的面积比为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
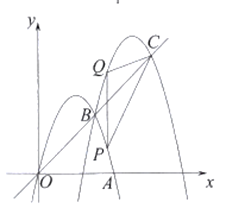
过C作CE⊥x轴于E,依据AB⊥x轴于点B,即可得出S△AOD=S四边形BDCE,证明△OBD∽△OEC,设△OBD的面积为S,则△OEC的面积为9S,△BDC的面积为2S,求出△ADO的面积为8S,即可得出△BDC与△ADO的面积比.
解:如图所示,过C作CE⊥x轴于E,
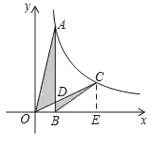
∵AB⊥x轴于点B,
∴S△AOB=S△COE,
∴S△AOD=S四边形BDCE,
∵BD∥CE,
∴△OBD∽△OEC,
∵CD=2OD,
∴![]() ,
,
设△OBD的面积为S,则△OEC的面积为9S,△BDC的面积为2S,
∴四边形BDCE的面积为8S,即△ADO的面积为8S,
∴△BDC与△ADO的面积比为2:8=1:4,
故选:B.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目