��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���O�İ뾶Ϊr��r��0�����������¶��壺��ƽ����һ��P��Բ��O�ľ���d������![]() ����Ƶ�PΪ��O�������ĵ�����
����Ƶ�PΪ��O�������ĵ�����
��1������O�İ뾶r=2ʱ��A��3��0����B��0��4����C��![]() ��2����D��
��2����D��![]() ��
��![]() ���У���O�������ĵ����� ��
���У���O�������ĵ����� ��
��2������E��4��3���ǡ�O�������ĵ��������O�İ뾶r��ȡֵ��Χ��
��3������O�İ뾶r=2ʱ��ֱ��y=- x+b��b��0����x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڡ�O�������ĵ�����ֱ��д��b��ȡֵ��Χ ��
���𰸡�(1) A,C ����2��![]() ��(3) 1��b��
��(3) 1��b��![]() ��-
��-![]() ��b��-1��
��b��-1��
��������
��1��������֪�������d�ķ�Χ��1��d��3���ٽ��������O��ľ��룬�����ж��Ƿ��ڴ˷�Χ�ڼ��ɣ����������ļ�Ϊ���ĵ㣻
��2�����ݵ�E��4��3���ǡ�O�������ĵ������ɸ���![]() �����d=5�������r�ķ�Χ���ɣ�
�����d=5�������r�ķ�Χ���ɣ�
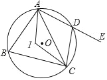
��3����ͼa��b��c��d����O�İ뾶r=2��������ĵ㷶Χ![]() ���ٷ������N��y��������ʱ������N��y�Ḻ����ʱ����������ۼ���.
���ٷ������N��y��������ʱ������N��y�Ḻ����ʱ����������ۼ���.
(1) �ߡ�O�İ뾶r=2��
��![]() =3��
=3��![]() =1
=1
��1��d��3
��A��3��0����
��OA=3���ڷ�Χ��
���A�ǡ�O�������ĵ���
��B��0��4��
��OB=4����4��3�����ڷ�Χ��
��B�Dz��ǡ�O�������ĵ�����
��C��![]() ��2����
��2����
��OC=![]() ���ڷ�Χ��
���ڷ�Χ��
���C�ǡ�O�������ĵ�����
��D��![]() ��
��![]() ����
����
��OD=![]() ��1�����ڷ�Χ��
��1�����ڷ�Χ��
���D���ǡ�O�������ĵ�����
�ʴ�Ϊ��A,C
��2���ߵ�E��4��3���ǡ�O�������ĵ���
��OE=5����d=5
��![]() �� ��r=10
�� ��r=10
�� ![]() ��
��![]()
��![]()
(3)
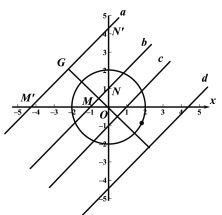
����ͼa��b��c��d����O�İ뾶r=2�����ĵ㷶Χ![]()
��![]()
��ֱ��MN�Ľ���ʽΪy=x+b��
��OM=ON��
�ٵ�N��y��������ʱ��
����M�ǡ�O�������ĵ�������ʱ����M��-1��0����
��M��-1��0������ֱ��MN�Ľ���ʽy=x+b�У���ã�b=1��
����b����СֵΪ1��
����O��OG��M'N'��G��
����G�ǡ�O�������ĵ���ʱ����ʱOG=3��
��Rt��ON'G����ON'G=45����
��GO=3
����Rt��GNN����![]() =
=![]() =
=![]() =
=![]() ��
��
b�����ֵΪ![]() ��
��
��1��b��![]() ��
��
�ڵ���N��y�Ḻ����ʱ��ͬ�ٵķ����ó�-![]() ��b��-1��
��b��-1��
����������b��ȡֵ��Χ�ǣ�1��b��![]() ��-
��-![]() ��b��-1��
��b��-1��

 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�