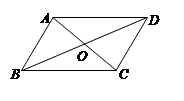题目内容
(12分)如图,△ABC和△ADC都是边长相等的等边三角形,点E、F同时分别从点B、 A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.
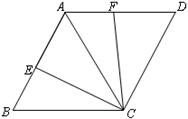
(1)写出在点E、F运动过程中,所有全等的三角形。
(2)点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(3)点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化吗?请说明理由;
(4)接EF,在图中找出和∠ACE相等的所有角,并说明理由.

(1)写出在点E、F运动过程中,所有全等的三角形。
(2)点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(3)点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化吗?请说明理由;
(4)接EF,在图中找出和∠ACE相等的所有角,并说明理由.
(1)
 (2)∠ECF不变为60°,理由见解析
(2)∠ECF不变为60°,理由见解析
(3)不变化,理由见解析(4)∠ACE=∠FCD=∠AFE.

 (2)∠ECF不变为60°,理由见解析
(2)∠ECF不变为60°,理由见解析(3)不变化,理由见解析(4)∠ACE=∠FCD=∠AFE.
(1)∵△ABC和△ADC都是边长相等的等边三角形,
∴
∵点E、F运动的速度相同,
∴AE=DF,BE=AF
∴

(2)∠ECF不变为60°.(1分)
理由如下:
∵△ABC和△ADC都是边长相等的等边三角形,
∴BC=AC=CD,∠B=∠DAC=60°,
又∵BE=AF,
∴△BCE≌△ACF,
∴∠ECB=∠FCA.(4分)
所以∠ECF=∠FCA+∠ACE=∠ECB+∠ACE=∠BCA=60°;(6分)
(3)不变化.理由如下:
∵四边形AECF的面积=△AFC的面积+△AEC的面积,(7分)
又∵△BCE≌△ACF,
∴△AEC的面积+△BEC的面积=△ABC的面积;(8分)
(4)证明:∵∠FCD+∠DFC=120°,∠AFE+∠DFC=120°,
∴∠AFE=∠FCD,
所以∠ACE=∠FCD=∠AFE.(10分)
(1)根据SSS求证 ,根据SAS求证
,根据SAS求证
 ;
;
(2)根据SAS证明△BCE≌△ACF,得到∠ECB=∠FCA,从而证明结论;
(3)结合(1)中证明的全等三角形,即可发现以点A、E、C、F为顶点的四边形的面积即为△ABC的面积;
(4)根据等边三角形的判定可以证明△ECF是等边三角形,再进一步根据平角定义,得到∠AFE+∠DFC=120°,则∠AFE=∠FCD,从而求解
∴

∵点E、F运动的速度相同,
∴AE=DF,BE=AF
∴


(2)∠ECF不变为60°.(1分)
理由如下:
∵△ABC和△ADC都是边长相等的等边三角形,
∴BC=AC=CD,∠B=∠DAC=60°,
又∵BE=AF,
∴△BCE≌△ACF,
∴∠ECB=∠FCA.(4分)
所以∠ECF=∠FCA+∠ACE=∠ECB+∠ACE=∠BCA=60°;(6分)
(3)不变化.理由如下:
∵四边形AECF的面积=△AFC的面积+△AEC的面积,(7分)
又∵△BCE≌△ACF,
∴△AEC的面积+△BEC的面积=△ABC的面积;(8分)
(4)证明:∵∠FCD+∠DFC=120°,∠AFE+∠DFC=120°,
∴∠AFE=∠FCD,
所以∠ACE=∠FCD=∠AFE.(10分)
(1)根据SSS求证
 ,根据SAS求证
,根据SAS求证
 ;
;(2)根据SAS证明△BCE≌△ACF,得到∠ECB=∠FCA,从而证明结论;
(3)结合(1)中证明的全等三角形,即可发现以点A、E、C、F为顶点的四边形的面积即为△ABC的面积;
(4)根据等边三角形的判定可以证明△ECF是等边三角形,再进一步根据平角定义,得到∠AFE+∠DFC=120°,则∠AFE=∠FCD,从而求解

练习册系列答案
相关题目