题目内容
【题目】阅读材料:
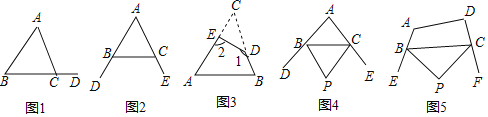
小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
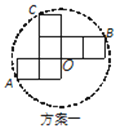
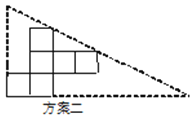
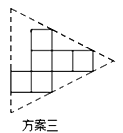
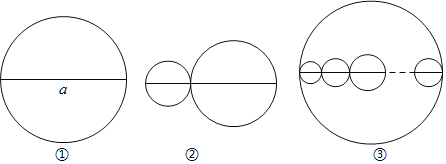
说明:方案一图形中的圆过点A,B,C,圆心O也是正方形的顶点;
回答问题(直接写出结果):
(1)方案二中,直角三角形纸片的两条直角边长分别为_______cm和_______cm;
(2)小明通过计算,发现方案一中纸片的利用率是________(填准确值),近似值约为38.2%.相比之下,方案二的利用率是________%.小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率是________.
【答案】(1)4cm;8cm;(2)![]() ;37.5;49.9%.
;37.5;49.9%.
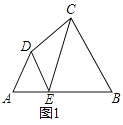
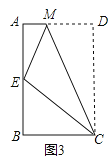
【解析】(1)如图,作辅助线,利用三角形全等和三角形相似对应边成比例,可以分别求得直角三角形的两个直角边的长度
(2)由(1)的结论直接可以得出结论,求得圆的半径后可以求得纸片的面积,从而利用展开图的面积除以总面积即可求得利用率;利用方案(3)的方法,分析求解即可求得答案.
(1)如图3:
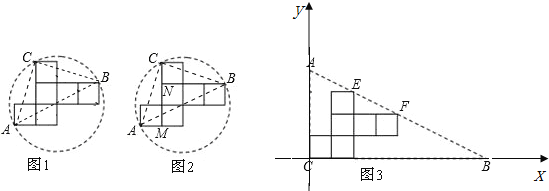
建立平面直角坐标系,可得E(2,3)、F(4,2)得直线解析式为y=-![]() x+4,
x+4,
∴A(0,4)B(8,0)
∴AC=4BC=8.
故答案为:4,8;
(2)∵由题意知:AB=2![]() ,
,
∴圆的半径为![]() ,
,
∴圆的面积为5π,
∵展开图的面积为6,
∴利用率=![]() ×100%=
×100%=![]() ×100%=
×100%=![]() ;
;
方案二:由(1)知,AC=4BC=8.
∴S△ACB=16.
∴该方案纸片利用率=![]() ×100%=
×100%=![]() ×100%=37.5%.
×100%=37.5%.
方案三:过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
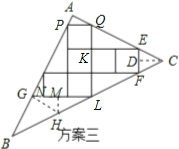
设AP=a,
∵PQ∥EK,
易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,
∴AP:AQ=QK:EK=1:2,
∴AQ=2a,PQ=![]() a,
a,
∴EQ=5a,
∵EC:ED=QE:QK,
∴EC=![]() a,
a,
则PG=5a+![]() a=
a=![]() a,GL=
a,GL=![]() a,
a,
∴GH=![]() a,
a,
∵![]() ,
,
解得:GB=![]() a,
a,
∴AB=![]() a,AC=
a,AC=![]() a,
a,
∴S△ABC=![]() ×AB×AC=
×AB×AC=![]() a2,
a2,
S展开图面积=6×5a2=30a2,
∴该方案纸片利用率=![]() ×100%=
×100%=![]() ×100%=49.86%≈49.9%.
×100%=49.86%≈49.9%.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案