题目内容
【题目】问题呈现
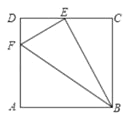
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
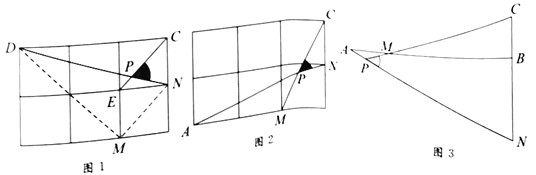
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
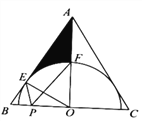
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】(1)根据方法归纳,运用勾股定理分别求出MN和DM的值,即可求出![]() 的值;
的值;
(2)仿(1)的思路作图,即可求解;
(3)方法同(2)
(1)如图进行构造
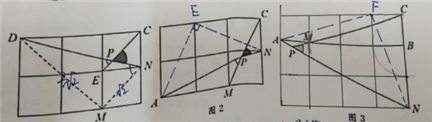
由勾股定理得:DM=![]() ,MN=
,MN=![]() ,DN=
,DN=![]()
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2
)2
∴DM2+MN2=DN2
∴△DMN是直角三角形.
∵MN∥EC
∴∠CPN=∠DNM,
∵tan∠DNM=![]() ,
,
∴![]() =2.
=2.
(2)![]()
∵![]() ,
,![]()
∴![]()
∴![]()
(3)![]() ,证明同(2).
,证明同(2).

练习册系列答案
相关题目
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

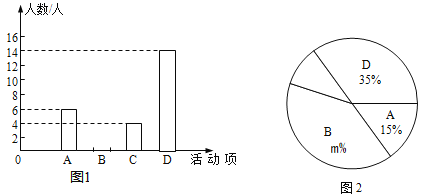
【题目】七(1)班同学为了解2017年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量 | 频数(户数) | 百分比 |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|

(1)请将下列频数分布表和频数分布直方图补充完整;
(2)求该小区月均用水量不超过![]() 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过![]() 的家庭数.
的家庭数.