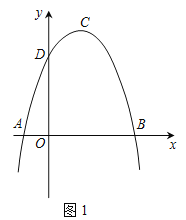题目内容
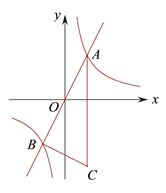
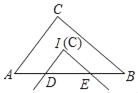
【题目】如图,![]() 中,
中,![]() 点
点![]() 与点
与点![]() 在
在![]() 的同侧,且
的同侧,且![]() .
.

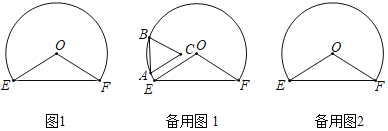
(1)如图1,点![]() 不与点
不与点![]() 重合,连结
重合,连结![]() 交
交![]() 于点
于点![]() .设
.设![]() 求
求![]() 关于
关于![]() 的函数解析式,写出自变量
的函数解析式,写出自变量![]() 的取值范围;
的取值范围;
(2)是否存在点![]() ,使
,使![]() 与
与![]() 相似,若存在,求
相似,若存在,求![]() 的长;若不存在,请说明理由;
的长;若不存在,请说明理由;
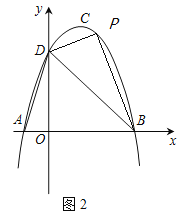
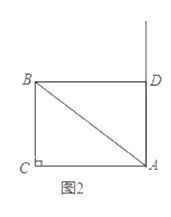
(3)如图2,过点![]() 作
作![]() 垂足为
垂足为![]() .将以点
.将以点![]() 为圆心,
为圆心,![]() 为半径的圆记为
为半径的圆记为![]() .若点
.若点![]() 到
到![]() 上点的距离的最小值为
上点的距离的最小值为![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)由AE⊥AC,∠ACB=90°,可得AE∥BC,然后由平行线分线段成比例定理,求得y关于x的函数解析式;
(2)由题意易得要使△PAE与△ABC相似,只有∠EPA=90°,即CE⊥AB,然后由△ABC∽△EAC,求得答案;
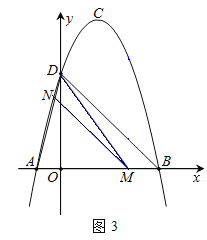
(3)易得点C必在⊙E外部,此时点C到⊙E上点的距离的最小值为CE-DE.然后分别从当点E在线段AD上时与当点E在线段AD延长线上时,去分析求解即可求得答案.
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,而
,而![]() 与
与![]() 都是锐角,
都是锐角,
![]() 要使
要使![]() 与
与![]() 相似,只有
相似,只有![]() ,
,
即![]()
此时![]() ,则
,则![]() ,
,
![]()
故存在点![]() ,使
,使![]() ,
,
此时![]()
![]() 点
点![]() 必在
必在![]() 外部,
外部,
![]() 此时点
此时点![]() 到
到![]() 上点的距离的最小值为
上点的距离的最小值为![]()
设![]()
①当点![]() 在线段
在线段![]() 上时,
上时,![]()
![]()
解得:![]()
即![]() 的半径为
的半径为![]()
②当点![]() 在线段
在线段![]() 延长线上时,
延长线上时,![]()
![]()
解得:![]()
即![]() 的半径为
的半径为![]()
![]()
![]() 的半径为
的半径为![]() 或
或![]()

练习册系列答案
相关题目