��Ŀ����
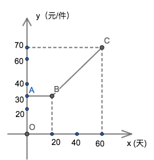
����Ŀ��Ϊʵ������������ⷢչ�����мƻ���ij��A��B���ౡ��ѧУȫ�����и��죮����Ԥ�㣬�����ʽ�1555��Ԫ����һ��A��ѧУ������B��ѧУ�����ʽ�230��Ԫ����������A��ѧУ��һ��B��ѧУ�����ʽ�205��Ԫ
��1������һ��A��ѧУ��һ��B��ѧУ������ʽ�ֱ��Ƕ�����Ԫ��
��2���������н����ֹ滮�ƻ�����Ը���A��B����ѧУ���и��죬Ҫ������A��ѧУ��B��ѧУ��2����2�����ڼƻ�Ͷ���ʽ���1555��Ԫ�������£������ܸ��������A��ѧУ��
���𰸡���1������һ��A��ѧУ������ʽ���60��Ԫ������һ��B��ѧУ������ʽ���85��Ԫ����2�������ܸ���16��A��ѧУ
��������
��1�������һ��A��ѧУ��һ��B��ѧУ������ʽ�ֱ���x��Ԫ��y��Ԫ�����������ж�Ԫһ�η����������⼴�ɣ�
��2�������B��ѧУa���������A��ѧУ![]() �������������г�һԪһ�β���ʽ������⼴��.
�������������г�һԪһ�β���ʽ������⼴��.
�⣺��1�������һ��A��ѧУ��һ��B��ѧУ������ʽ�ֱ���x��Ԫ��y��Ԫ����������ɵã�
![]()
��ã�![]()
�𣺸���һ��A��ѧУ������ʽ���60��Ԫ������һ��B��ѧУ������ʽ���85��Ԫ��
��2�������B��ѧУa���������A��ѧУ![]() �������ݾ���ɵã�
�������ݾ���ɵã�
![]()
��ã�![]()
��![]()
�������ܸ���16��A��ѧУ��

 �Ķ��쳵ϵ�д�
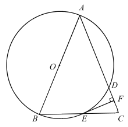
�Ķ��쳵ϵ�д�����Ŀ����ͼ1��M��Բ��![]() ��һ���㣬P����AB��һ���㣬����A������MP�Ĵ��߽�Բ�ڵ�C������PC����֪AB��5cm����A��P�����ľ���Ϊxcm��A��C�����ľ���Ϊy1cm��P��C����ľ���Ϊy2cm��С˧����ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
��һ���㣬P����AB��һ���㣬����A������MP�Ĵ��߽�Բ�ڵ�C������PC����֪AB��5cm����A��P�����ľ���Ϊxcm��A��C�����ľ���Ϊy1cm��P��C����ľ���Ϊy2cm��С˧����ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С˧��̽�����̣��벹��������
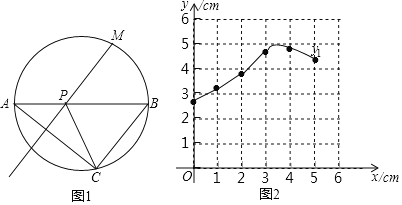
��1�����ձ����Ա���x��ֵ����ȡ�㣬��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.55 | 3.15 | 3.95 | 4.76 | 4.95 | 4.30 |
y2/cm | 2.55 | 2.64 | 2.67 | �� �� | 1.13 | 2.55 |
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��
��3����Ϻ���ͼ������⣺�ڵ�P���˶������У���AC��PC�IJ�Ϊ���ֵʱ��AP�ij���ԼΪ�� ��cm��