题目内容
如图,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,则这条抛物线的关系式为______.


当x=0时,y=2,所以B点的坐标是(0,2),
当y=0时,x=-2,所以A点的坐标是(-2,0),
∴OA=OB,∴∠OAB=45°,
∵∠ABC=90°,
∴∠OAB=∠OCB=45°,
∴OC=OB=OA=2,
∴C点的坐标是(2,0),
设抛物线的表达式为y=a(x-2)2,抛物线过B(0,2),
所以4a=2,a=
,
因此抛物线的解析式为:y=
(x-2)2=
x2-2x+2.
当y=0时,x=-2,所以A点的坐标是(-2,0),
∴OA=OB,∴∠OAB=45°,
∵∠ABC=90°,
∴∠OAB=∠OCB=45°,
∴OC=OB=OA=2,
∴C点的坐标是(2,0),
设抛物线的表达式为y=a(x-2)2,抛物线过B(0,2),
所以4a=2,a=
| 1 |
| 2 |
因此抛物线的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

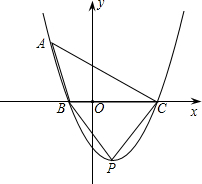

 半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.