题目内容
已知抛物线y=ax2-2ax+c-1的顶点在直线y=-
x+8上,与x轴相交于B(α,0)、C(β,0)两点,其中α<β,且α2+β2=10.
(1)求这个抛物线的解析式;
(2)设这个抛物线与y轴的交点为P,H是线段BC上的一个动点,过H作HK∥PB,交PC于K,连接PH,记线段BH的长为t,△PHK的面积为S,试将S表示成t的函数;
(3)求S的最大值,以及S取最大值时过H、K两点的直线的解析式.
| 8 |
| 3 |
(1)求这个抛物线的解析式;
(2)设这个抛物线与y轴的交点为P,H是线段BC上的一个动点,过H作HK∥PB,交PC于K,连接PH,记线段BH的长为t,△PHK的面积为S,试将S表示成t的函数;
(3)求S的最大值,以及S取最大值时过H、K两点的直线的解析式.
(1)由y=ax2-2ax+c-1=a(x-1)2+c-1-a得抛物线的顶点为
A(1,c-1-a).
∵点A在直线y=-
x+8上,
∴c-1-a=-
×1+8,
即c=a+
,①
又抛物线与x轴相交于B(α,0)、C(β,0)两点,
∴α、β是方程ax2-2ax+c-1=0的两个根.
∴α+β=2,αβ=
,
又α2+β2=10,即(α+β)2-2αβ=10,
∴4-2×
=10,
即c=1-3a②,
由①②解得:a=-
,c=5,
∴y=-
x2+
x+4,
此时,抛物线与x轴确有两个交点,
答:这个抛物线解析式为:y=-
x2+
x+4.
(2)由抛物线y=-
x2+
x+4,
令x=0,得y=4,故P点坐标为(0,4),
令y=0,解得x1=-1,x2=3,
∵α<β,∴B(-1,0),C(3,0),
∴BC=4,又由OC=3,OP=4,得PC=5,sin∠BCP=
=
,
∵BH=t,∴HC=4-t.
∵HK∥BP,
=
,
=
,
∴PK=
t
如图,过H作HG⊥PC于G,则HG=HC,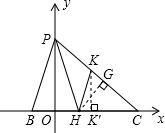
sin∠BCP=(4-t)•
=
(4-t),
∴S=
×
t×
(4-t)=
t2+2t,
∵点H在线段BC上且HK∥BP,∴0<t<4.
∴所求的函数式为:S=-
t2+2t(0<t<4),
答:将S表示成t的函数为S=-
t2+2t(0<t<4).
(3)由S=-
t2+2t=-
(t-2)2+2(0<t<4),知:
当t=2(满足0<t<4)时,S取最大值,其值为2,
此时,点H的坐标为(1,0),
∵HK∥PB,且H为BC的中点,
∴K为PC的中点,
作KK′⊥HC于K′,
则KK′=
PO=2,OK′=
CO=
,
∴点K的坐标为(
,2),
设所求直线的解析式为y=kx+b,则
,
∴
故所求的解析式为y=4x-4,
答S的最大值是2,S取最大值时过H、K两点的直线的解析式是y=4x-4.
A(1,c-1-a).
∵点A在直线y=-
| 8 |
| 3 |
∴c-1-a=-
| 8 |
| 3 |
即c=a+
| 19 |
| 3 |
又抛物线与x轴相交于B(α,0)、C(β,0)两点,
∴α、β是方程ax2-2ax+c-1=0的两个根.
∴α+β=2,αβ=
| c-1 |
| a |
又α2+β2=10,即(α+β)2-2αβ=10,
∴4-2×
| c-1 |
| a |
即c=1-3a②,
由①②解得:a=-
| 4 |
| 3 |
∴y=-
| 4 |
| 3 |
| 8 |
| 3 |
此时,抛物线与x轴确有两个交点,
答:这个抛物线解析式为:y=-
| 4 |
| 3 |
| 8 |
| 3 |
(2)由抛物线y=-
| 4 |
| 3 |
| 8 |
| 3 |
令x=0,得y=4,故P点坐标为(0,4),
令y=0,解得x1=-1,x2=3,
∵α<β,∴B(-1,0),C(3,0),
∴BC=4,又由OC=3,OP=4,得PC=5,sin∠BCP=
| OP |
| PC |
| 4 |
| 5 |
∵BH=t,∴HC=4-t.
∵HK∥BP,
| BH |
| HC |
| PK |
| KC |
| t |
| 4-t |
| PK |
| 5-PK |
∴PK=
| 5 |
| 4 |
如图,过H作HG⊥PC于G,则HG=HC,

sin∠BCP=(4-t)•
| 4 |
| 5 |
| 4 |
| 5 |
∴S=
| 1 |
| 2 |
| 5 |
| 4 |
| 4 |
| 5 |
| 1 |
| 2 |
∵点H在线段BC上且HK∥BP,∴0<t<4.
∴所求的函数式为:S=-
| 1 |
| 2 |
答:将S表示成t的函数为S=-
| 1 |
| 2 |
(3)由S=-
| 1 |
| 2 |
| 1 |
| 2 |
当t=2(满足0<t<4)时,S取最大值,其值为2,
此时,点H的坐标为(1,0),
∵HK∥PB,且H为BC的中点,
∴K为PC的中点,
作KK′⊥HC于K′,
则KK′=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴点K的坐标为(
| 3 |
| 2 |
设所求直线的解析式为y=kx+b,则
|
∴
|
故所求的解析式为y=4x-4,
答S的最大值是2,S取最大值时过H、K两点的直线的解析式是y=4x-4.

练习册系列答案
相关题目

 x轴的负半轴交于点B,且S△OAB=a.
x轴的负半轴交于点B,且S△OAB=a.



 积为常数时,矩形ABCD需要满足什么条件并说明理由.
积为常数时,矩形ABCD需要满足什么条件并说明理由. 园的面积y(米2)与x(米)的关系式为______.(不要求写出自变量x的取值范围)
园的面积y(米2)与x(米)的关系式为______.(不要求写出自变量x的取值范围)