题目内容
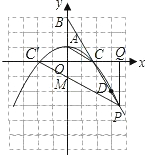
已知等腰三角形ABC的两个顶点分别是A(0,1)、B(0,3),第三个顶点C在x轴的正 半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
(1)求直线BC的解析式;
(2)求抛物线y=ax2+bx+c的解析式及点P的坐标;
(3)设M是y轴上的一个动点,求PM+CM的取值范围.
 半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.(1)求直线BC的解析式;
(2)求抛物线y=ax2+bx+c的解析式及点P的坐标;
(3)设M是y轴上的一个动点,求PM+CM的取值范围.
(1)∵A(0,1),B(0,3),
∴AB=2,
∵△ABC是等腰三角形,且点C在x轴的正半轴上,
∴AC=AB=2,
∴OC=
=
.
∴C(
,0).(2分)
设直线BC的解析式为y=kx+3,
∴
k+3=0,
∴k=-
.
∴直线BC的解析式为y=-
x+3.(4分)
(2)∵抛物线y=ax2+bx+c关于y轴对称,
∴b=0.(5分)
又抛物线y=ax2+bx+c经过A(0,1),D(3,-2)两点.
∴
解得
∴抛物线的解析式是y=-
x2+1.(7分)
在Rt△AOC中,OA=1,AC=2,易得∠ACO=30°.
在Rt△BOC中,OB=3,OC=
,易得∠BCO=60°.
∴CA是∠BCO的角平分线.
∴直线BC与x轴关于直线AC对称.
点P关于直线AC的对称点在x轴上,则符合条件的点P就是直线BC与抛物线y=-
x2+1的交点.(8分)
∵点P在直线BC:y=-
x+3上,故设点P的坐标是(x,-
x+3).
又∵点P(x,-
x+3)在抛物线y=-
x2+1上,
∴-
x+3=-
x2+1.
解得x1=
,x2=2
.
故所求的点P的坐标是P1(
,0),P2(2
,-3).(10分)
(3)要求PM+CM的取值范围,可先求PM+C′M的最小值.
(I)当点P的坐标是OC=
时,点P与点C重合,
故PM+CM=2CM.
显然CM的最小值就是点C到y轴的距离为
,
∵点M是y轴上的动点,
∴PM+CM无最大值,
∴PM+CM≥2
.(13分)
(II)当点P的坐标是(2
,-3)时,由点C关于y轴的对称点C′(-
,0),
故只要求PM+MC'的最小值,显然线段PC'最短.易求得PC'=6.
∴PM+CM的最小值是6.
同理PM+CM没有最大值,
∴PM+CM的取值范围是PM+CM≥6.
综上所述,当点P的坐标是(
,0)时,PM+CM≥2
,
当点P的坐标是(2
,-3)时,PM+CM≥6.(15分)
∴AB=2,
∵△ABC是等腰三角形,且点C在x轴的正半轴上,
∴AC=AB=2,
∴OC=
| AC2-OA2 |
| 3 |
∴C(
| 3 |
设直线BC的解析式为y=kx+3,
∴
| 3 |
∴k=-
| 3 |
∴直线BC的解析式为y=-
| 3 |
(2)∵抛物线y=ax2+bx+c关于y轴对称,
∴b=0.(5分)
又抛物线y=ax2+bx+c经过A(0,1),D(3,-2)两点.
∴
|
解得
|
∴抛物线的解析式是y=-
| 1 |
| 3 |
在Rt△AOC中,OA=1,AC=2,易得∠ACO=30°.
在Rt△BOC中,OB=3,OC=
| 3 |
∴CA是∠BCO的角平分线.
∴直线BC与x轴关于直线AC对称.
点P关于直线AC的对称点在x轴上,则符合条件的点P就是直线BC与抛物线y=-
| 1 |
| 3 |
∵点P在直线BC:y=-
| 3 |
| 3 |
又∵点P(x,-
| 3 |
| 1 |
| 3 |
∴-
| 3 |
| 1 |
| 3 |
解得x1=
| 3 |
| 3 |
故所求的点P的坐标是P1(
| 3 |
| 3 |
(3)要求PM+CM的取值范围,可先求PM+C′M的最小值.
(I)当点P的坐标是OC=
| 3 |
故PM+CM=2CM.
显然CM的最小值就是点C到y轴的距离为
| 3 |
∵点M是y轴上的动点,
∴PM+CM无最大值,
∴PM+CM≥2
| 3 |
(II)当点P的坐标是(2
| 3 |
| 3 |
故只要求PM+MC'的最小值,显然线段PC'最短.易求得PC'=6.
∴PM+CM的最小值是6.
同理PM+CM没有最大值,
∴PM+CM的取值范围是PM+CM≥6.
综上所述,当点P的坐标是(
| 3 |
| 3 |
当点P的坐标是(2
| 3 |


练习册系列答案
相关题目






 线
线