Question

在平面直角坐标系中，已知抛物线y=-x²+bx+c与x轴交于点A（-1，0）、B（3，0），与y轴的正半轴交于点C，顶点为E．
（1）求抛物线解析式及顶点E的坐标；
（2）如图，过点E作BC平行线，交x轴于点F，在不添加线和字母情况下，图中面积相等的三角形有：______；
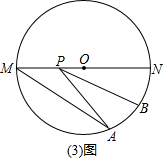
（3）将抛物线向下平移，与x轴交于点M、N，与y轴的正半轴交于点P，顶点为Q．在四边形MNQP中满足S_△NPQ=S_△MNP，求此时直线PN的解析式．

Answer 1

（1）将A（-1，0）、B（3，0）代入y=-x²+bx+c的得

0=-1-b+c 0=-9+3b+c

，
解得：

b=2 c=3

∴抛物线的解析式为y=-x²+2x+3，
即y=-（x-1）²+4．
∴抛物线顶点E的坐标为（1，4）；

（2）∵EF∥BC，
∴△BCF与△BCE的BC边上的高相等，
S_△BCF=S_△BCE．

（3）将抛物线向下平移，则顶点Q在对称轴x=1上，
∴-

b

2a

=1，
∴-

b

-2

=1，
∴b=2，
设抛物线的解析式为y=-x²+2x+c（c＞0）．
∴此时，抛物线与y轴的交点为P（0，c），顶点为Q（1，1+c）．
∴OP=c，DQ=1+c．
∵y=0时
∴-x²+2x+c=0，
∴x1=1-

1+c

，x2=1+

1+c

，
∴M(1-

1+c

，0)，N(1+

1+c

，0)．
如图，过点Q作QG∥PN与x轴交于点G，连接NG，则S_△PNG=S_△PNQ．
∵S_△NPQ=S_△MNP，
∴S_△MNP=S_△PNG．
∴NG=MN=2

1+c

．
设对称轴x=1与x轴交于点D，
∴DG=

1

2

MN+NG=3

1+c

．
∵QG∥PN，
∴∠PND=∠QGD．
∴Rt△QDG∽Rt△PON．
∴

QD

DG

=

PO

ON

．
∴

1+c

3 1+c

=

c

1+ 1+c

．
c=

5

4

．
∴点P(0，

5

4

)，N(

5

2

，0)．
设直线PN的解析式为y=mx+n，将P，N两点代入，得

5 4 =n 0= 5 2 +n

，
解得：

m=-- 1 2 n= 5 4

∴直线PN的解析式为y=-

1

2

x+

5

4

．
故答案为：△BCF与△BCE．