题目内容
【题目】装厂批发某种服装，每件成本为65元，规定不低于10件可以批发，其批发价y（元/件）与批发数量x（件）（x为正整数）之间所满足的函数关系如图所示．
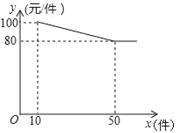
(1)求y与x之间所满足的函数关系式，并写出x的取值范围；
(2)若10≤x≤50（x为正整数），求批发该种服装多少件时，服装厂获得利润600元？
【答案】（1）
；
（2）60件．
【解析】
（1）根据题意和函数图象可以写出y与x之间所满足的函数关系式，并写出x的取值范围；
（2）根据题意可以得到利润600与x的函数关系式，然后根据二次函数的性质，即可解答本题．
解：（1）当10≤x≤50时，设y与x的函数关系式为y=kx+b，
，解之得
，
∴当10≤x≤50时，y与x的函数关系式为y=-0.5x+105，
当x＞50时，y=80，
即y与x的函数关系式为： ；
（2）设批发该种服装
件，
由题意可得：
，
解之得：
，或
（不合题意，舍去），
∴当批发该种服装60件时，服装厂获得利润600元．
练习册系列答案
相关题目
【题目】对于抛物线
.
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
x | … | … | |||||
y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程
（t为实数）在
＜x＜
的范围内有解，则t的取值范围是 ．
