Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ‘ŕľ◊““ŃĹłŲ≤ĽÕł√ųĶńŅŕīŁ÷–£¨∑÷Īū”–īů–°°Ę≤ń÷ ÕÍ»ęŌŗÕ¨Ķń–°«Ú£¨∆š÷–ľ◊ŅŕīŁ÷–Ķń–°«Ú…Ō∑÷ĪūĪÍ”– ż◊÷1£¨2£¨3£¨4£¨““ŅŕīŁ÷–Ķń–°«Ú…Ō∑÷ĪūĪÍ”– ż◊÷2£¨3£¨4£¨Ō»ī”ľ◊īŁ÷–»ő“‚√Ģ≥Ų“ĽłŲ–°«Ú£¨ľ«Ō¬ ż◊÷ő™m£¨‘Ŕī”““īŁ÷–√Ģ≥Ų“ĽłŲ–°«Ú£¨ľ«Ō¬ ż◊÷ő™n£ģ
£®1£©«Ž”√Ń–ĪŪĽÚĽ≠ ų◊īÕľĶń∑Ĺ∑®ĪŪ ĺ≥Ųňý”–£®m£¨n£©Ņ…ń‹ĶńĹŠĻŻ£Ľ
£®2£©»Űm£¨n∂ľ «∑Ĺ≥Őx2©Ā5x+6£Ĺ0ĶńĹ‚ Ī£¨‘Ú–°√ųĽŮ §£Ľ»Űm£¨n∂ľ≤Ľ «∑Ĺ≥Őx2©Ā5x+6£Ĺ0ĶńĹ‚ Ī£¨‘Ú–°ņŻĽŮ §£¨ő ňŻ√«ŃĹ»ňň≠ĽŮ §ĶńłŇ¬ īů£Ņ
°ĺīūįł°Ņ£®1£©Ļ≤”–12łŲĶ»Ņ…ń‹ĶńĹŠĻŻ£¨ľŻĹ‚őŲ£Ľ£®2£©–°√ų°Ę–°ņŻĽŮ §ĶńłŇ¬ “Ľ—ýīů£ģ
°ĺĹ‚őŲ°Ņ
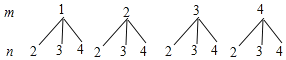
£®1£© ◊Ō»łýĺ›Ő‚“‚Ľ≠≥Ų ų◊īÕľ£¨»Ľļů”… ų◊īÕľŅ…Ķ√ňý”–Ņ…ń‹ĶńĹŠĻŻ£Ľ
£®2£©Ľ≠ ų◊īÕľ’Ļ ĺňý”–6÷÷Ķ»Ņ…ń‹ĶńĹŠĻŻ ż£¨‘Ŕ’“≥Ų ż◊÷÷ģĽżń‹ĪĽ2’Ż≥żĶńĹŠĻŻ ż£¨»Ľļůłý図Ҭ Ļę Ĺ«ůĹ‚£ģ
Ĺ‚£ļ£®1£© ų◊īÕľ»ÁÕľňý ĺ£ļ
£®2£©°Ŗm£¨n∂ľ «∑Ĺ≥Őx2©Ā5x+6£Ĺ0ĶńĹ‚£¨
°ŗm£Ĺ2£¨n£Ĺ3£¨ĽÚm£Ĺ3£¨n£Ĺ2£¨
”… ų◊īÕľĶ√£ļĻ≤”–12łŲĶ»Ņ…ń‹ĶńĹŠĻŻ£¨m£¨n∂ľ «∑Ĺ≥Őx2©Ā5x+6£Ĺ0ĶńĹ‚ĶńĹŠĻŻ”–2łŲ£¨
m£¨n∂ľ≤Ľ «∑Ĺ≥Őx2©Ā5x+6£Ĺ0ĶńĹ‚ĶńĹŠĻŻ”–2łŲ£¨
–°√ųĽŮ §ĶńłŇ¬ ő™![]() £¨–°ņŻĽŮ §ĶńłŇ¬ ő™
£¨–°ņŻĽŮ §ĶńłŇ¬ ő™![]() £¨
£¨
°ŗ–°√ų°Ę–°ņŻĽŮ §ĶńłŇ¬ “Ľ—ýīů£ģ

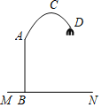
°ĺŐ‚ńŅ°Ņ–Ū∂ŗľ“Õ•“‘»ľ∆Ý◊ųő™…’ňģ◊Ų∑ĻĶń»ľŃŌ£¨Ĺŕ‘ľ”√∆Ý «ő“√«»’≥£…ķĽÓ÷–∑«≥£Ō÷ ĶĶńő Ő‚.ń≥ŅÓ»ľ∆Ý‘Ó–żŇ•őĽ÷√ī”0∂»ĶĹ90∂»£¨»ľ∆ÝĻōĪ’ Ī£¨»ľ∆Ý‘Ó–żŇ•őĽ÷√ő™0∂»£¨–żŇ•Ĺ«∂»‘Ĺīů£¨»ľ∆ÝŃųŃŅ‘Ĺīů£¨»ľ∆ÝŅ™ĶĹ◊Óīů Ī£¨–żŇ•Ĺ«∂»ő™90∂».ő™≤‚ ‘»ľ∆Ý‘Ó–żŇ•‘ŕ≤ĽÕ¨őĽ÷√…ŌĶń»ľ∆Ý”√ŃŅ£¨‘ŕŌŗÕ¨ŐűľĢŌ¬£¨—°‘ّ໾∆Ý‘Ó–żŇ•Ķń5łŲ≤ĽÕ¨őĽ÷√…Ō∑÷Īū…’Ņ™“ĽļÝňģ£®ĶĪ–żŇ•Ĺ«∂»Őę–° Ī£¨∆šĽūѶ≤Ľń‹ĻĽĹęňģ…’Ņ™£¨Ļ —°‘Ů–żŇ•Ĺ«∂»![]() ∂»Ķń∑∂őß «
∂»Ķń∑∂őß «![]() £©£¨ľ«¬ľŌŗĻō żĺ›Ķ√ĶĹŌ¬ĪŪ£ļ
£©£¨ľ«¬ľŌŗĻō żĺ›Ķ√ĶĹŌ¬ĪŪ£ļ
–żŇ•Ĺ«∂»£®∂»£© | 20 | 50 | 70 | 80 | 90 |
ňý”√»ľ∆ÝŃŅ£®…ż£© | 73 | 67 | 83 | 97 | 115 |
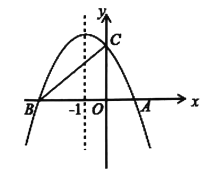
£®1£©«Žń„ī”ňý—ßŌįĻżĶń“ĽīőļĮ ż°Ę∑īĪ»ņżļĮ żļÕ∂ĢīőļĮ ż÷–»∑∂®ńń÷÷ļĮ żń‹ĪŪ ĺňý”√»ľ∆ÝŃŅ![]() …ż”Ž–ż◊™Ĺ«∂»
…ż”Ž–ż◊™Ĺ«∂»![]() ∂»ĶńĪšĽĮĻś¬…£ŅňĶ√ų»∑∂®’‚÷÷ļĮ ż∂Ý≤Ľ «∆šňŻļĮ żĶńņŪ”…£¨≤Ę«ů≥ŲňŁĶńĹ‚őŲ Ĺ£Ľ
∂»ĶńĪšĽĮĻś¬…£ŅňĶ√ų»∑∂®’‚÷÷ļĮ ż∂Ý≤Ľ «∆šňŻļĮ żĶńņŪ”…£¨≤Ę«ů≥ŲňŁĶńĹ‚őŲ Ĺ£Ľ
£®2£©ĶĪ–ż◊™Ĺ«∂»ő™∂ŗ…Ŕ Ī£¨…’Ņ™“ĽļÝňģňý”√»ľ∆ÝŃŅ◊Ó…Ŕ£Ņ◊Ó…Ŕ «∂ŗ…Ŕ£Ņ
£®3£©ń≥ľ“Õ• Ļ”√īňŅÓ»ľ∆Ý‘Ó£¨“‘«įŌįĻŖį—»ľ∆ÝŅ™ĶĹ◊Óīů£¨Ō÷≤…”√◊ÓĹŕ °»ľ∆ÝĶń–ż◊™Ĺ«∂»£¨»Űł√ľ“Õ•Ō÷‘ŕ√Ņ‘¬Ķń∆Ĺĺý»ľ∆Ý”√ŃŅő™13ŃĘ∑Ĺ√◊£¨«ůŌ÷‘ŕ√Ņ‘¬∆Ĺĺýń‹Ī»“‘«į√Ņ‘¬Ĺŕ °»ľ∆Ý∂ŗ…ŔŃĘ∑Ĺ√◊£Ņ