题目内容
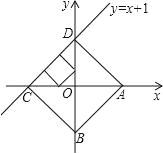
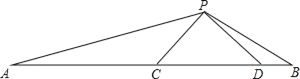
【题目】如图：△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°
求证：（1）△PAC∽△BPD；
（2）若AC=3，BD=1，求CD的长．
【答案】（1）见解析；（2）
.
【解析】
（1）由△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°，可得∠PAB=∠PBD，∠BPD=∠PAC，从而即可证明；
（2）根据相似三角形对应边成比例即可求出PC=PD=
，再由勾股定理即可求解．
证明：（1）∵△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°，
∴∠APC+∠BPD=45°，
又∠PAB+∠PBA=45°，∠PBA+∠PBD=45°，
∴∠PAB=∠PBD，∠BPD=∠PAC，
∵∠PCA=∠PDB，
∴△PAC∽△BPD；
（2）∵
，PC=PD，AC=3，BD=1
∴PC=PD=，
∴CD=
．
【题目】近几年“雾霾”成为全社会关注的话题某校环保志愿者小组对该市2018年空气质量进行调查，从全年365天中随机抽查了50天的空气质量指数（AQI），得到以下数据：43、62、80、78、46、78、23、59、32、78、86、125、98、116、86、69、28、43、58、87、75、116、178、146、57、26、43、59、77、103、126、159、201、289、315、253、196、102、93、72、56、43、39、44、47、34、31、29、43、52．
（1）请你完成如下的统计表；
AQI | 0～50 | 51～100 | 101～150 | 151～200 | 201～250 | 300以上 |
质量等级 | A（优） | B（良） | C（轻度污染） | D（中度污染） | E（重度污染） | F（严重污染） |
天数 |
（2）请你根据题中所给信息绘制该市2018年空气质量等级条形统计图；
（3）请你估计该市全年空气质量等级为“重度污染”和“严重污染”的天数．
