题目内容
【题目】在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
(1)抛物线的对称轴为直线x=-3,AB=4.求抛物线的表达式;
(2)平移(1)中的抛物线,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;
(3)当m=4时,抛物线上有两点M(x1,y1)和N(x2,y2),若x1<2,x2>2,x1+x2>4,试判断y1与y2的大小,并说明理由.
【答案】(1)y=-x2-6x-5.(2)点P的坐标(1,1).(3)y1>y2.
【解析】
(1)先根据抛物线和x轴的交点及线段的长,求出抛物线的解析式;
(2)根据平移后抛物线的特点设出抛物线的解析式,再利用等腰直角三角形的性质求出抛物线解析式;
(3)根据抛物线的解析式判断出点M,N的大概位置,再关键点M,N的横坐标的范围即可得出结论.
(1)抛物线y=-x2+mx+n的对称轴为直线x=-3,AB=4.
∴点A(-5,0),点B(-1,0).
∴抛物线的表达式为y=-(x+5)(x+1)
∴y=-x2-6x-5.
(2)如图1,
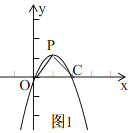
依题意,设平移后的抛物线表达式为:y=-x2+bx.
∴抛物线的对称轴为直线x=![]() ,抛物线与x正半轴交于点C(b,0).
,抛物线与x正半轴交于点C(b,0).
∴b>0.
记平移后的抛物线顶点为P,
∴点P的坐标(![]() ,
,![]() ),
),
∵△OCP是等腰直角三角形,
∴![]() =
=![]()
∴b=2.
∴点P的坐标(1,1).
(3)如图2,
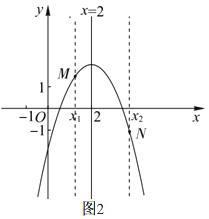
当m=4时,抛物线表达式为:y=-x2+4x+n.
∴抛物线的对称轴为直线x=2.
∵点M(x1,y1)和N(x2,y2)在抛物线上,
且x1<2,x2>2,
∴点M在直线x=2的左侧,点N在直线x=2的右侧.
∵x1+x2>4,
∴2-x1<x2-2,
∴点M到直线x=2的距离比点N到直线x=2的距离近,
∴y1>y2.

 阅读快车系列答案
阅读快车系列答案