题目内容
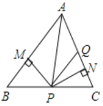
【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。其中正确的个数有( )

A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】
试题由AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,结合公共边AD,可证得△ADF≌△ADE,根据全等三角形的性质再结合FB=CE,依次分析个小题即可.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵DE⊥AC,DF⊥AB
∴∠AFD=∠AED=90°
∵AD=AD
∴△ADF≌△ADE
∴DE=DF,AE=AF
∵FB=CE
∴AB=AC
∵∠BAD=∠CAD,AD=AD
∴△ABD≌△ACD
∴BD=CD,∠ADB=∠ADC=90°
∴AD⊥BC
故选D.

练习册系列答案
相关题目