题目内容
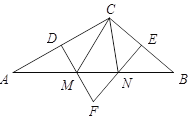
【题目】如图.在不等边△ABC中,PM⊥AB,垂足为M,PN⊥AC,垂足为N,且PM=PN,Q在AC上,PQ=QA,下列结论.①AN=AM,②QP∥AM,③△BMP≌△QNP,其中正确的是( )
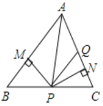
A.①②③B.①②C.②③D.①
【答案】B
【解析】
利用“HL”证明△APM和△APN全等,根据全等三角形对应边相等可得AN=AM;全等三角形对应角相等可得∠PAM=∠PAN,再根据等边对等角可得∠PAN=∠APQ,从而得到∠PAM=∠APQ,然后根据内错角相等,两直线平行可得QP∥AM;欲证△BMP和△QNP全等,须得BP=PQ=AQ,从而得到AC=BC,而此条件无法得到,所以,两三角形不一定全等.
∵PM⊥AB,PN⊥AC,
∴∠AMP=∠ANP=90°,
在Rt△APM和Rt△APN中,![]()
∴Rt△APM≌Rt△APN(HL),
∴AN=AM,故①正确;
∠PAM=∠PAN,
∵PQ=QA,
∴∠PAN=∠APQ,
∴∠PAM=∠APQ,
∴QP∥AM,故②正确;
假设△BMP≌△QNP,
则BP=PQ,
∵PQ=QA,
∴BP=PQ=AQ,
又∵QP∥AM,
∴AC=BC,
此条件无法从题目得到,
所以,假设不成立,故③错误.
综上所述,正确的是①②.
故选B.

练习册系列答案
相关题目