Question

【题目】两角分别相等的两个三角形___________．

Answer 1

【答案】相似

【解析】

首先，通过作平行线，依据平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似，可以判定所作△A'DE与△A'B'C'相似；然后，再依据相似三角形的对应角相等和已知条件可以证明所作△A'DE与△ABC全等；最后，可证得△ABC∽△A'B'C'．

已知：如图，在△ABC和△A'B'C'中，∠A=∠A'，∠B=∠B'．

求证：△ABC∽△A'B'C'．

证明：在线段A'B'上截取A'D=AB，过点D作DE∥B'C'，交A'C'于点E．

由此得到△A'DE∽△A'B'C'．

∴∠A'DE=∠B'．

∵∠B=∠B'，

∴∠A'DE=∠B．

∵∠A'=∠A，

∴△A'DE≌△ABC．

∴△ABC∽△A'B'C'．

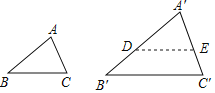
故答案为相似.