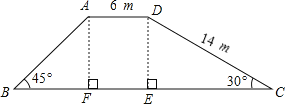
题目内容
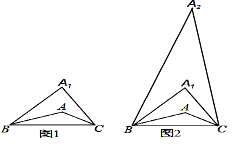
【题目】如图，有
、
、
三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
【答案】B
【解析】
要求到三小区的距离相等，首先思考到A小区、C小区距离相等，根据线段垂直平分线定理的逆定理，满足条件的点在线段AC的垂直平分线上，同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上，即可得到答案.
解：根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等．
∴超市应建在AC，BC两边垂直平分线的交点处．
故选择：B.
练习册系列答案
相关题目
【题目】某公司根据市场计划调整投资策略，对A、B两种产品进行市场调查，收集数据如下表：
项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
A | 20 | m | 10 | 200 |
B | 40 | 8 | 18 | 120 |
其中，m是待定系数，其值是由生产A的材料的市场价格决定的，变化范围是6≤m＜8，销售B产品时需缴纳
x2万元的关税．其中，x为生产产品的件数．假定所有产品都能在当年售出，设生产A，B两种产品的年利润分别为y1、y2（万元）．
（1）写出y1、y2与x之间的函数关系式，注明其自变量x的取值范围．
（2）请你通过计算比较，该公司生产哪一种产品可使最大年利润更大？
