题目内容
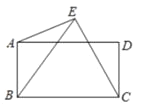
【题目】如图，
分别是正方形
的边
的中点，以
为边作正方形
，
与
交于点
，联结
．
（1）求证：
；
（2）设
，求证
．
【答案】（1）见解析；（2）见解析
【解析】
（1）先说明△ADE≌△DCF,然后再利用同角的余角相等以及垂直的定义即可证明；
（2）先证△ADE∽△ECQ，得出
，进而可得△AEQ∽△ADE∽△ECQ，然后根据相似三角形的性质即可证明．
（1）证明：∵四边形ABCD是正方形
∴AD=DC，∠ADE=∠DCF=90°
在△ADE和△DCF中
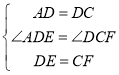
∴△ADE≌△DCF（SAS）
∴∠EAD=∠CDF
∵∠AED+∠EAD=90°
∴∠AED+∠CDF=90°
∴AE⊥DF；
（2）∵∠ADE=∠C，∠CEQ=∠EAD，
∴△ADE∽△ECQ
∵E是CD的中点
∴，
∵∠ADE=∠C=90°
∴△AEQ∽△ADE∽△ECQ
设CE
，则AD=2a，AE=
∴
，
，
∴
．
练习册系列答案
名校课堂系列答案
相关题目
