题目内容
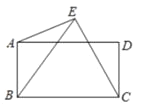
【题目】如图,在矩形ABCD中,AB=5,BC=8,在AB的右侧有一点E,且AE=AB,BE=BC,则CE=________.
【答案】![]()
【解析】
过点E作EH⊥BC于点H,过点A作AG⊥BE于点G,可推出∠AGB=∠BHE=90°,利用等腰三角形的性质求出BG的长,利用勾股定理求出AG的长;再利用矩形的性质去证明∠EBH=∠BAG,从而可以得到△ABG∽△BEH,利用相似三角形的对应边成比例,求出EH,BH的长,继而可求出CH的长,然后在Rt△CEH中,利用勾股定理求出CE的长.
解:过点E作EH⊥BC于点H,过点A作AG⊥BE于点G,
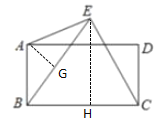
∴∠AGB=∠BHE=90°,
∵AE=AB,BE=BC=8,
∴BG=![]() BE=
BE=![]() ×8=4,
×8=4,
∴![]() ,
,
∵矩形ABCD,
∴∠EBH+∠ABG=90°,∠ABG+∠BAG=90°,
∴∠EBH=∠BAG,
∴△ABG∽△BEH,
∴![]() 即
即![]() ,
,
解之:![]() ,
,
∴CH=BC-BH=![]() ;
;
在Rt△CEH中,
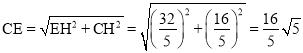 .
.
故答案为:![]() .
.

练习册系列答案
相关题目