题目内容
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.为了了解垃圾分类知识的普及情况,某校随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成下面两幅不完整的统计图:
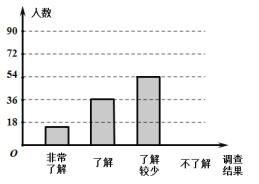
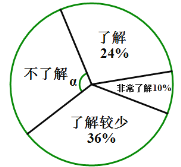
(1)本次被调查的学生有 名,扇形统计图中,![]()
(2)将条形统计图剩余的部分补充完整(包括朱标记的数据)
(3)估计该校![]() 名学生中“非常了解”与“了解”的人数和是多少.
名学生中“非常了解”与“了解”的人数和是多少.
(4)某环保小队有3名男生,1名女生,从中随机抽取2人在全校做垃圾分类知识交流,求恰好抽到一男一女的概率.
【答案】(1)![]() ;(2)见解析;(3)952;(4)树状图见解析,
;(2)见解析;(3)952;(4)树状图见解析,![]()
【解析】
(1)先由了解的人数及其所占百分比求出总人数,再根据各项目的百分比之和为1求出不了解对应的百分比,用360°乘以不了解对应的百分比可得答案;
(2)用总人数分别乘以非常了解、了解较少、不了解对应的百分比求出其人数,据此可补全图形;
(3)用总人数乘以两者百分比之和即可得;
(4)画树状图展示所有12种等可能的结果数,找出抽到一男一女的结果数,然后根据概率公式求解.
(1)本次被调查的学生有36÷24%=150(名),
∵“不了解”对应的百分比为1-(24%+10%+36%)=30%,
∴扇形统计图中,∠α=360°×30%=108°,
故答案为:150、108°;
(2)非常了解的人数为150×10%=15(名),
了解较少的人数为150×36%=54(名),
不了解的人数为150×30%=45(名),
补全图形如下:

![]() 估计该校
估计该校![]() 名学生中“非常了解”与“了解”的人数和是
名学生中“非常了解”与“了解”的人数和是![]() (名);
(名);
![]() 可以画树状图为:
可以画树状图为:
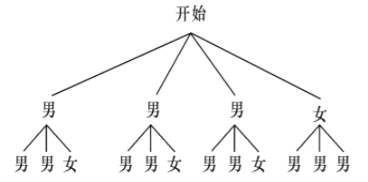
共有![]() 种等可能的结果,其中抽到
种等可能的结果,其中抽到![]() 男
男![]() 女的结果数为
女的结果数为![]()
所以恰好抽到一男一女的概率为![]()

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目