Question

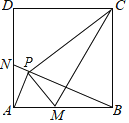
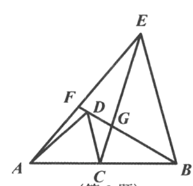
【题目】如图，在线段AB上有一点C,在AB的同侧作等腰△ACD和等腰△ECB,且AC=AD,EC=EB,∠DAC=∠CEB,直线BD与线段AE,线段CE分别交于点F,G.对于下列结论：①△DCG∽△BEG；②△ACE∽△DCB；③GF·GB=GC·GE；④若∠DAC=∠CEB=90°,则2AD2=DF·DG.其中正确的是（ ）

A.①②③④B.①②③C.①③④D.①②

Answer 1

【答案】A

【解析】

利用三角形的内角和定理及两组角分别相等证明①正确；根据两组边成比例夹角相等判断②正确；利用③的相似三角形证得∠AEC=∠DBC,又对顶角相等，证得③正确；根据△ACE∽△DCB证得F、E、B、C四点共圆，由此推出△DCF∽△DGC，列比例线段即可证得④正确.

①正确；在等腰△ACD和等腰△ECB中AC=AD,EC=EB,∠DAC=∠CEB,

∴∠ACD=∠ADC=∠BCE=∠BEC,

∴∠DCG=180-∠ACD-∠BCE=∠BEC,

∵∠DGC=∠BGE,

∴△DCG∽△BEG;

②正确；∵∠ACD+∠DCG=∠BCE+∠DCG,

∴∠ACE=∠DCB,

∵,

∴△ACE∽△DCB；

③正确；∵△ACE∽△DCB，

∴∠AEC=∠DBC,

∵∠FGE=∠CGB,

∴△FGE∽△CGB,

∴GF·GB=GC·GE；

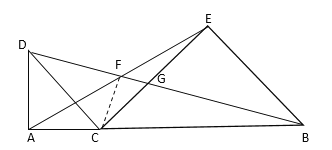
④正确；如图，连接CF,

由②可得△ACE∽△DCB，

∴∠AEC=∠DBC,

∴F、E、B、C四点共圆，

∴∠CFB=∠CEB=90，

∵∠ACD=∠ECB=45，

∴∠DCE=90，

∴△DCF∽△DGC

∴,

∴,

∵,

∴2AD2=DF·DG.

故选：A.