题目内容
【题目】已知三点A（0，0），B（5，12），C（14，0），则△ABC内心的坐标为____．
【答案】（6，4）．
【解析】
作BQ⊥AC于点Q，由题意可得BQ=12，根据勾股定理分别求出BC、AB的长，继而利用三角形面积，可得△OAB内切圆半径，过点P作PD⊥AC于D，PF⊥AB于F，PE⊥BC于E，设AD=AF=x，则CD=CE=14-x，BF=13-x，BE=BC-CE=15-（14-x）=1+x，由BF=BE可得13-x=1+x，解之求出x的值，从而得出点P的坐标，即可得出答案．
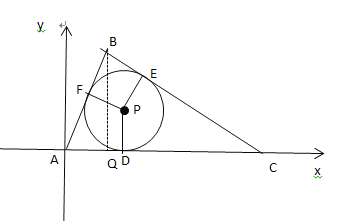
解：如图，过点B作BQ⊥AC于点Q，
则AQ=5，BQ=12，
∴AB=
，CQ=AC-AQ=9，
∴BC=
设⊙P的半径为r，根据三角形的面积可得：r=
过点P作PD⊥AC于D，PF⊥AB于F，PE⊥BC于E，
设AD=AF=x，则CD=CE=14-x，BF=13-x，
∴BE=BC-CE=15-（14-x）=1+x，
由BF=BE可得13-x=1+x，
解得：x=6，
∴点P的坐标为（6，4），
故答案为：（6，4）．
练习册系列答案
相关题目
