题目内容
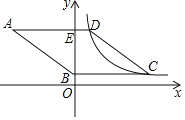
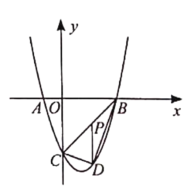
【题目】抛物线y=ax2-4ax+4(a≠0)与y轴交于点A.过点B(0,3)作y轴的垂线l,若抛物线y=ax2-4ax+4(a≠0)与直线l有两个交点,设其中靠近y轴的交点的横坐标为m,且│m│<1,则a的取值范围是______.
【答案】a>![]() 或a<
或a<![]() .
.
【解析】
先确定抛物线的对称轴,根据开口的大小与a的关系,即开口向上时,a>0,且a越大开口越小,开口向下时,a<0,且a越大,开口越大,从而确定a的范围.
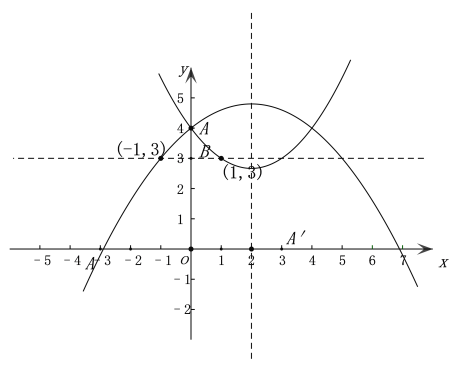
解:如图,观察图形
抛物线y=ax2-4ax+4的对称轴为直线![]() ,
,
设抛物线与直线l交点(靠近y轴)为(m,3),
∵│m│<1,
∴-1<m<1.
当a>0时,若抛物线经过点(1,3)时,开口最大,此时a值最小,
将点(1,3)代入y=ax2-4ax+4,
得,3=a-4a+4
解得a=![]() ,
,
∴a>![]() ;
;
当a<0时,若抛物线经过点(-1,3)时,开口最大,此时a值最大,
将点(-1,3)代入y=ax2-4ax+4,
得,3=a+4a+4
解得a=![]() ,
,
∴a<![]() .
.
a的取值范围是a>![]() 或a<
或a<![]() .
.
故答案为:a>![]() 或a<
或a<![]() .
.

练习册系列答案
相关题目