Question

【题目】如图，在正方形ABCD中，N为边AD上一点，连接BN．过点A作AP⊥BN于点P，连接CP，M为边AB上一点，连接PM，∠PMA＝∠PCB，连接CM，有以下结论：①△PAM∽△PBC；②PM⊥PC；③M、P、C、B四点共圆；④AN＝AM．其中正确的个数为（　　）

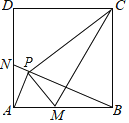
A.4B.3C.2D.1

Answer 1

【答案】A

【解析】

根据互余角性质得∠PAM＝∠PBC，进而得△PAM∽△PBC，可以判断①；

由相似三角形得∠APM＝∠BPC，进而得∠CPM＝∠APB，从而判断②；

根据对角互补，进而判断③；

由△APB∽△NAB得，再结合△PAM∽△PBC便可判断④．

解：∵AP⊥BN，

∴∠PAM+∠PBA＝90°，

∵∠PBA+∠PBC＝90°，

∴∠PAM＝∠PBC，

∵∠PMA＝∠PCB，

∴△PAM∽△PBC，

故①正确；

∵△PAM∽△PBC，

∴∠APM＝∠BPC，

∴∠CPM＝∠APB＝90°，即PM⊥PC，

故②正确；

∵∠MPC+∠MBC＝90°+90°＝180°，

∴B、C、P、M四点共圆，

∴∠MPB＝∠MCB，

故③正确；

∵AP⊥BN，

∴∠APN＝∠APB＝90°，

∴∠PAN+∠ANB＝90°，

∵∠ANB+∠ABN＝90°，

∴∠PAN＝∠ABN，

∵∠APN＝∠BPA＝90°，

∴△PAN∽△PBA，

∴，

∵△PAM∽△PBC，

∴，

∴，

∵AB＝BC，

∴AM＝AN，

故④正确；

故选：A．