Question

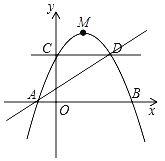
【题目】如图，抛物线y＝ax2+bx﹣1经过A（﹣0.5，0），B（﹣4，﹣3）两点，交y轴于点C．

（1）求抛物线的表达式；

（2）若点P是抛物线对称轴上一动点，求使得PA+PC最小时P点的坐标；

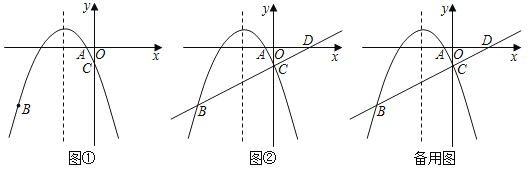
（3）直线BC交x轴于点D，连结AC，若点P是y轴上一动点，且点P不与点C重合，是否存在点P，使得以P，B，C为顶点的三角形与△ACD相似？若存在，确定点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）（﹣，﹣）；（3）（0，﹣3）或（0，﹣11）

【解析】

（1）把A（﹣0.5，0），B（﹣4，3）代入解析式即可求得结果；

（2）由（1）可得函数解析式，令y=0得到与x轴的交点，得出CD直线坐在的解析式，根据对称的性质即可求解；

（3）由点B、C的坐标可得直线BC的表达式，可得△ACD为直角三角形，且∠ACD＝90°，若以P，B，C为顶点的三角形与△ACD相似相似，则可分两种情况考虑，①当∠BPC＝90°，②当∠PBC＝90°时，即可求解；

解：（1）∵抛物线y＝ax2+bx﹣1经过A（﹣0.5，0），B（﹣4，3）两点，

∴，

解得，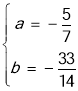

∴；

（2）由（1）知，令y＝0，得x1＝﹣2.8，x2＝﹣0.5，

又A（﹣0.5，0），

∴抛物线与x轴另一交点为E（﹣2.8，0），而点C（0，﹣1），

连接CE交函数对称轴于点P，则点P为所求点，

∴由点C、D的坐标，可得直线CE表达式为：，

又抛物线对称轴为直线，

∴使得PA+PC最小时P点的坐标为（﹣，﹣ ）；

（3）由点B、C的坐标可得，直线BC的表达式为：y＝x﹣1，故D（2，0），

∵tan∠ADC＝＝tan∠ACO，

∴∠ADC＝∠CAO，

又∠ODC+∠OCD＝90°，

∴∠ACO+∠OCD＝90°，

∴△ACD为直角三角形且∠ACD＝90°，

由点A、D的坐标得：AD＝2.5，

同理可得：AC＝，CD＝，

∴AC2+CD2＝AD2，

∴△ACD为直角三角形，且∠ACD＝90°，

若以P，B，C为顶点的三角形与△ACD相似相似，则可分两种情况考虑：

①当∠BPC＝90°，

即BP⊥y轴时，

△CPB∽△ACD，

∴P（0，﹣3）；

②当∠PBC＝90°时，

△CBP∽△ACD，

过点B作BF⊥y轴于点F，

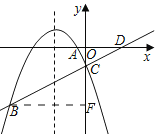
在Rt△BFC中，BF＝4，CF＝2，

则BC＝，

∵，

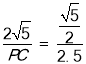∴，解得：PC＝10，

∴OP＝11，

∴P（0，﹣11），

综合以上可得P点的坐标为（0，﹣3）或（0，﹣11）．