题目内容
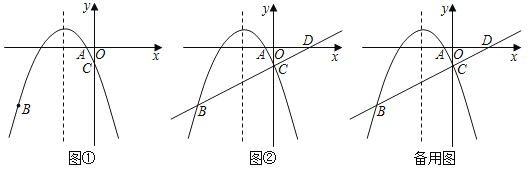
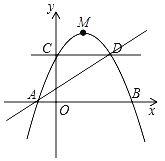
【题目】如图,已知顶点为M(![]() ,
,![]() )的抛物线过点D(3,2),交x轴于A,B两点,交y轴于点C,点P是抛物线上一动点.
)的抛物线过点D(3,2),交x轴于A,B两点,交y轴于点C,点P是抛物线上一动点.
(1)求抛物线的解析式;
(2)当点P在直线AD上方时,求△PAD面积的最大值,并求出此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q'.是否存在点P,使Q'恰好落在x轴上?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)最大值为4,点P(1,3);(3)存在,点P的坐标为(
;(2)最大值为4,点P(1,3);(3)存在,点P的坐标为(![]() ,
,![]() ).
).
【解析】
(1)用待定系数法求解即可;
(2)由△PAD面积S=S△PHA+S△PHD,即可求解;
(3)结合图形可判断出点P在直线CD下方,设点P的坐标为(a,![]() ),当P点在y轴右侧时,运用解直角三角形及相似三角形的性质进行求解即可.
),当P点在y轴右侧时,运用解直角三角形及相似三角形的性质进行求解即可.
解:(1)设抛物线的表达式为:y=a(x﹣h)2+k=a(x﹣![]() )2+
)2+![]() ,
,
将点D的坐标代入上式得:2=a(3﹣![]() )2+
)2+![]() ,
,
解得:a=﹣![]() ,
,
∴抛物线的表达式为:![]() ;
;
(2)当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
即点C坐标为(0,2),
同理,令y=0,则x=4或﹣1,故点A、B的坐标分别为:(﹣1,0)、(4,0),
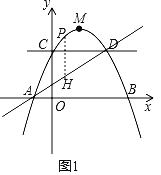
过点P作y轴的平行线交AD于点H,
由点A、D的坐标得,直线AD的表达式为:y=![]() (x+1),
(x+1),
设点P(x,﹣![]() x2+
x2+![]() x+2),则点H(x,
x+2),则点H(x,![]() x+
x+![]() ),
),
则△PAD面积为:
S=S△PHA+S△PHD=![]() ×PH×(xD﹣xA)=
×PH×(xD﹣xA)=![]() ×4×(﹣
×4×(﹣![]() x2+
x2+![]() x+2﹣
x+2﹣![]() x
x![]() )=﹣x2+2x+3,
)=﹣x2+2x+3,
∵﹣1<0,故S有最大值,
当x=1时,S有最大值,则点P(1,3);
(3)存在满足条件的点P,显然点P在直线CD下方,设直线PQ交x轴于F,点P的坐标为(a,﹣![]() a2+
a2+![]() a+2),
a+2),
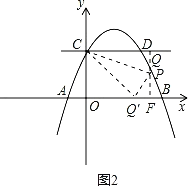
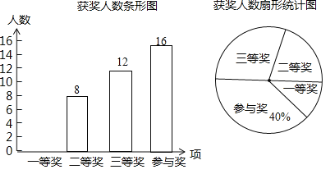
当P点在y轴右侧时(如图2),CQ=a,
PQ=2﹣(﹣![]() a2+
a2+![]() a+2)=
a+2)=![]() a2﹣
a2﹣![]() a,
a,
又∵∠CQ′O+∠FQ′P=90°,∠COQ′=∠Q′FP=90°,
∴∠FQ′P=∠OCQ′,
∴△COQ′∽△Q′FP,
![]() ,即
,即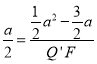 ,
,
∴Q′F=a﹣3,
∴OQ′=OF﹣Q′F=a﹣(a﹣3)=3,CQ=CQ′=![]() ,
,
此时a=![]() ,点P的坐标为(
,点P的坐标为(![]() ,
,![]() ).
).

 发散思维新课堂系列答案
发散思维新课堂系列答案