题目内容
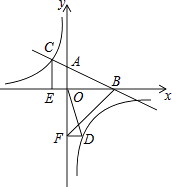
【题目】点E为正方形ABCD边BC上的一点,点G为BC延长线一点,连接AE,过点E作AE⊥EF,且AE=EF,连接CF.
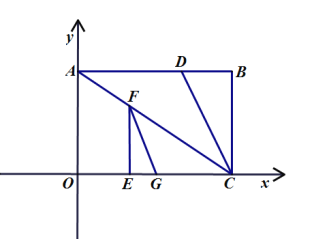
(1)如图1,求证:∠FCG=45°,
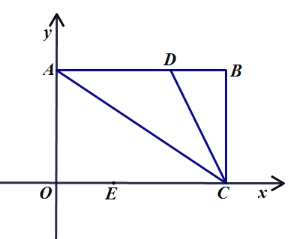
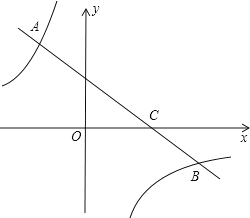
(2)如图2,过点D作DH//EF交AB于点H,连接HE,求证:![]() ;
;
(3)如图3,连接AF、DF,若AF交CD于点M,DM=2,BH=3,求DF的长.

【答案】(1)见解析;(2)见解析;(3)3![]() .
.
【解析】
(1)过点F作FK⊥CG于点K,证出![]() ≌
≌![]() ,得到BE=HF,再根据正四边形的性质得到BC=AB=EH,从而计算出EH-EC=BC-EC,即BE=CH,故CH=HF,再根据∠CHF=90°,求出∠FCG=45°;
,得到BE=HF,再根据正四边形的性质得到BC=AB=EH,从而计算出EH-EC=BC-EC,即BE=CH,故CH=HF,再根据∠CHF=90°,求出∠FCG=45°;
(2)利用角边角定理证明△DAH≌△ABE,从而得到AH=BE,然后利用勾股定理进行证明;
(3)过点A作AO⊥AM交BC延长线于点O,连接EM,证![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,结合△DAH≌△ABE,证平行四边形HEFD,从而得到DF=HE ,设AH=BE=x,OE=EM=2+x,CM=x+1,然后在Rt△ECM中,利用勾股定理列方程求解.
,结合△DAH≌△ABE,证平行四边形HEFD,从而得到DF=HE ,设AH=BE=x,OE=EM=2+x,CM=x+1,然后在Rt△ECM中,利用勾股定理列方程求解.
解:(1)过点F作FK⊥CG于点K,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠FEK=90°,
又∵∠BAE+∠AEB=90°,
∴∠FEK=∠EAB,
又∵∠B=∠EKF,
且AE=EF,
∴△ABE≌△EKF,
∴BE=KF,BC=AB=EK,
∴EK-EC=BC-EC,
∴BE=CK,
∴CK=KF.
∴∠FCK=∠CFK=![]()
(2) ∵DH∥EF,AE⊥EF
∴AE⊥DH
∴∠EAD+∠ADH=90°
又∵正方形ABCD中,∠BAD=90°,AD=AB,∠DAB=∠B=90°
∴∠BAE+∠EAD=90°
∴∠BAE=∠ADH
∴△DAH≌△ABE
∴AH=BE
∵在Rt△BHE中,![]()
∴![]()
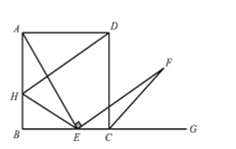
(3)过点A作AO⊥AM交BC延长线于点O,连接EM.
∵OA⊥AM,
∴∠OAM=90°
又因为正方形ABCD中,AB=AD,∠BAD=∠ABC=∠ADC=90°
∴∠OAM=∠BAD
∴∠OAM-∠BAM=∠BAD-∠BAM
∴∠OAB=∠MAD
∴![]() ≌
≌![]()
∴AO=AM
∵AE⊥EF,且AE=EF
∴∠EAM=45°
∴∠MAD+∠BAE=45°
∴∠OAB+∠BAE=45°
∴∠OAE=∠EAM
又∵AE=AE
∴![]() ≌
≌![]()
∴OE=EM
由(2)可知△DAH≌△ABE
∴DH=AE
∴DH=EF,且DH//EF
∴四边形HEFD为平行四边形,
∴DF=HE
设AH=BE=x,OE=EM=OB+DE=DM+BE2+x,CM=CD-DM=x+1,
∴在Rt△ECM中,![]() ,解得x=3
,解得x=3
在Rt△BEH中,![]()
∴DF=3![]() .
.