题目内容
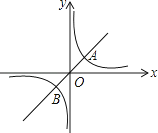
【题目】如图,一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.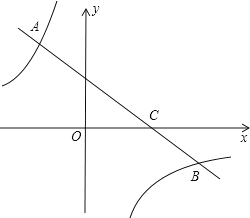
(1)求该一次函数的解析式;
(2)若反比例函数y=![]() 的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
【答案】
(1)
解:∵一次函数y=kx+b(k<0)的图象经过点C(3,0),
∴3k+b=0①,点C到y轴的距离是3,
∵k<0,
∴b>0,
∵一次函数y=kx+b的图象与y轴的交点是(0,b),
∴![]() ×3×b=3,
×3×b=3,
解得:b=2.
把b=2代入①,解得:k=![]() ,则函数的解析式是y=
,则函数的解析式是y=![]() x+2.
x+2.
故这个函数的解析式为y=![]() x+2;
x+2;
(2)
解:如图,
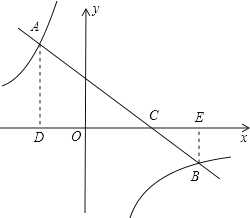
作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.
∵AD∥BE,
∴△ACD∽△BCE,
∴![]() =2,
=2,
∴AD=2BE.
设B点纵坐标为﹣n,则A点纵坐标为2n.
∵直线AB的解析式为y=![]() x+2,
x+2,
∴A(3﹣3n,2n),B(3+![]() n,﹣n),
n,﹣n),
∵反比例函数y=![]() 的图象经过A、B两点,
的图象经过A、B两点,
∴(3﹣3n)2n=(3+![]() n)(﹣n),
n)(﹣n),
解得n1=2,n2=0(不合题意舍去),
∴m=(3﹣3n)2n=﹣3×4=﹣12.
【解析】(1)先由一次函数y=kx+b(k<0)的图象经过点C(3,0),得出3k+b=0①,由于一次函数y=kx+b的图象与y轴的交点是(0,b),根据三角形的面积公式可求得b的值,然后利用待定系数法即可求得函数解析式;
(2)作AD⊥x轴于点D,BE⊥x轴于点E,则AD∥BE.由△ACD∽△BCE,得出![]() =2,那么AD=2BE.设B点纵坐标为﹣n,则A点纵坐标为2n.由直线AB的解析式为y=﹣
=2,那么AD=2BE.设B点纵坐标为﹣n,则A点纵坐标为2n.由直线AB的解析式为y=﹣![]() x+2,得出A(3﹣3n,2n),B(3+
x+2,得出A(3﹣3n,2n),B(3+![]() n,﹣n),再根据反比例函数y=
n,﹣n),再根据反比例函数y=![]() 的图象经过A、B两点,列出方程(3﹣3n)2n=(3+
的图象经过A、B两点,列出方程(3﹣3n)2n=(3+![]() n)(﹣n),解方程求出n的值,那么m=(3﹣3n)2n,代入计算即可.
n)(﹣n),解方程求出n的值,那么m=(3﹣3n)2n,代入计算即可.

 阅读快车系列答案
阅读快车系列答案