题目内容
【题目】在平面直角坐标系之中,点O为坐标原点,直线![]() 分别交x、y轴于点B、A,直线
分别交x、y轴于点B、A,直线![]() 与直线
与直线![]() 交于点C.
交于点C.
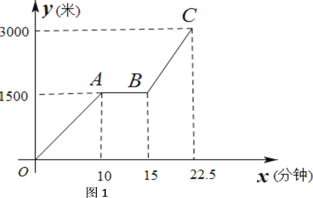
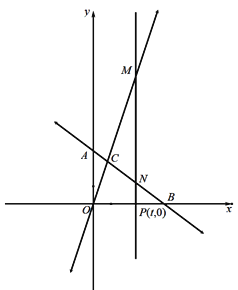
(1)如图1,求点C的坐标.
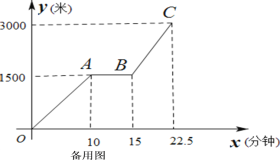
(2)如图2,点P(t,0)为C点的右侧x轴上一点,过点P作x轴垂线分别交AB、OC于点N、M,若MN=5NP,求t的值.
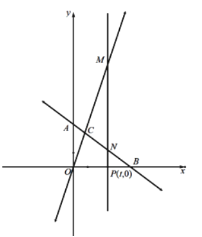
(3)如图3,点F为平面内任意一点,是否存在y轴正半轴上一点E,使点E、F、M、N围成的四边形为菱形,若存在求出点E坐标;若不存在,请说明理由.



【答案】(1)C![]() ;(2)t=2.4 ; (3)
;(2)t=2.4 ; (3)![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
【解析】
(1)联立正比例函数与一次函数解析式组成方程组,求出方程组的解得到x与y的值,确定出C点坐标即可;
(2)设P(t,0),则N(t,![]() ),M(t,3t),利用两点间距离公式表示出MN,NP的长,然后根据题意列方程求解;
),M(t,3t),利用两点间距离公式表示出MN,NP的长,然后根据题意列方程求解;
(3)根据t的值求出点M,N的坐标和MN的长度,然后分MN为对角线或MN为边结合菱形的性质和勾股定理进行分情况讨论求解.
解:(1)∵直线![]() 与直线
与直线![]() 交于点C.
交于点C.
∴联立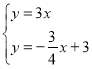 ,解得
,解得![]()
∴C![]()
(2)设P(t,0),则N(t,![]() ),M(t,3t)
),M(t,3t)
MN=3t-(![]() )=
)=![]() , NP=
, NP=![]()
∵MN=5NP,
∴![]() =5(
=5(![]() ),
),
解得t=2.4
(3)经过计算:当t=2.4 时,M(![]() ),N(
),N(![]() ),MN=6,
),MN=6,
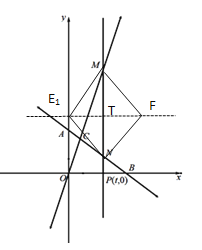
情况1,以MN为对角线,作MN的垂直平分线交y轴正半轴于点E,
∴MT=NT=3,ET=TF=2.4,
∴此时![]() ,即
,即![]()
情况2:以MN为边,点E在点M的下面,![]() ,
,
作![]() ⊥MN,∴
⊥MN,∴![]()
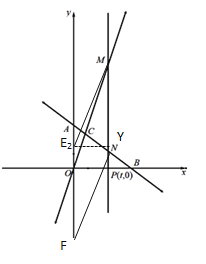
在Rt△![]() 中,MY=
中,MY=![]() ,
,
∴此时![]()
情况3:以MN为边,点E在点M的上面![]()
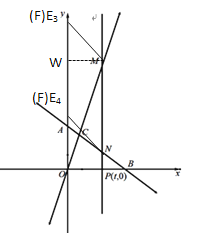
同理作![]() ⊥MN,解得MW=
⊥MN,解得MW=![]() ,
,
此时![]() 或
或![]() .
.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目