题目内容
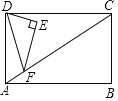
【题目】如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)见解析;(2) 图中阴影部分的面积为![]() .
.
【解析】
(1)连接OF,AO,根据题意可得∠ABF=∠AFB=∠EBF=30°,再利用OB=OF,证明AB∥OF,即可解答
(2)先利用等弧对等角求出△AOF是等边三角形,再证明S△ABF=S△AOF,即可解答
(1)证明:连接OF,AO,
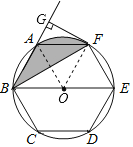
∵AB=AF=EF,
∴![]() ,
,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵![]() ,
,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2![]() ,
,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积=![]() .
.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
【题目】某校为了解九年级学生的体育达标情况,随机抽取![]() 名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
测试成绩(分) |
|
|
|
|
|
人数(人) |
|
|
|
|
|
(1)该校九年级有![]() 名学生,估计体育测试成绩为
名学生,估计体育测试成绩为![]() 分的学生人数;
分的学生人数;
(2)该校体育老师要对本次抽测成绩为![]() 分的甲、乙、丙、丁
分的甲、乙、丙、丁![]() 名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)